Computer Science/Data Structure
[자료구조] Graph: 개념, Vertices/Edges, 종류, 트리구조와 비교, 표현 (Adjacency Matrix vs Adjacency List)
깃짱
2023. 12. 20. 17:00
반응형
반응형
Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS
GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip
주니어 개발자를 위한 전공 지식 모음.zip. Contribute to seoul-developer/CS development by creating an account on GitHub.
github.com
💋 Graph란?
✔️ 개념
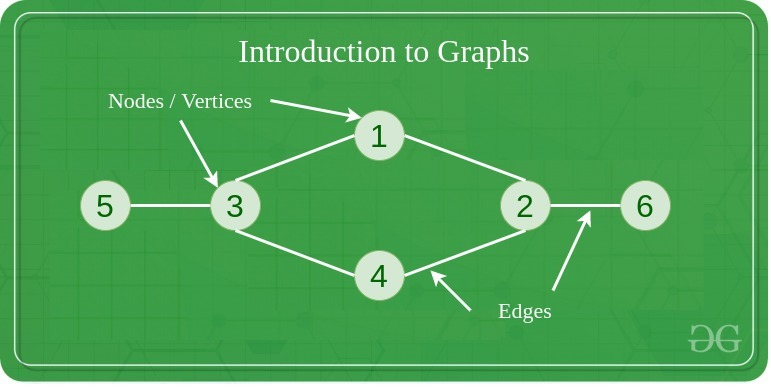
node(정점)과edge(간선)으로 구성된비선형데이터 구조node의 집합(V)과edge의 집합(E)으로 이루어져 있다 ⇒G(E, V)로 표기
✔️ 구성 요소
- Vertices
- nodes, 정점으로도 부른다.
- 그래프의 기본 단위
- 각 노드는 레이블이 지정될 수도 있고 되지 않을 수도 있습니다.
- Edges
- arcs, 간선으로도 부른다.
- 두 노드를 연결하는 데 사용되는 선이나 링크
- 어떤 방식으로든 그래프의 두 노드를 연결할 수 있으며, 규칙이 없다.
- 각 간선은 레이블이 지정될 수도 있고 되지 않을 수도 있습니다.
💋 Graph의 종류
- 무방향 그래프 (Undirected Graph) vs 방향 그래프 (Directed Graph 또는 Digraph)
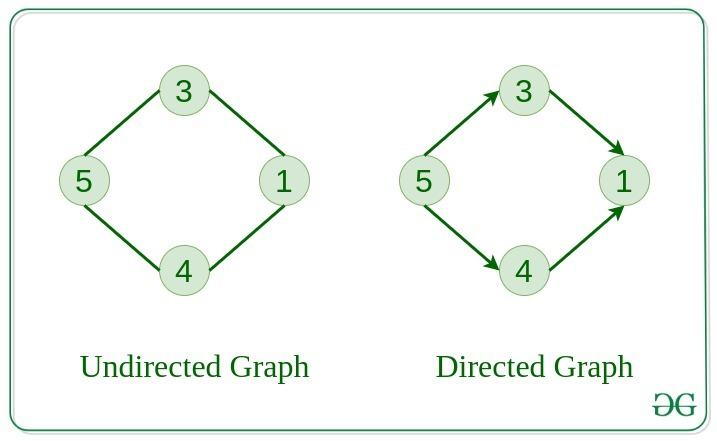
- 가중치 그래프 (Weighted Graph)
- 간선에 가중치 또는 가중값이 할당된 그래프입니다. 가중치는 간선의 가중치를 나타내는 숫자입니다.
- 무방향 가중치 그래프 (Undirected Weighted Graph)
- 방향이 없는 그래프이면서, 간선에 가중치가 할당된 그래프
- 방향 가중치 그래프 (Directed Weighted Graph)
- 방향이 있는 그래프이면서, 간선에 가중치가 할당된 그래프
- 사이클이 없는 그래프 (Acyclic Graph)
- 그래프 내에 순환 구조가 없는 그래프
- 예. 트리
- 사이클이 있는 그래프 (Cyclic Graph) vs 사이클 그 자체인 그래프 (Cycle Graph)
- Cyclic Graph는 그래프 내에 적어도 하나 이상의 순환 구조가 있는 그래프
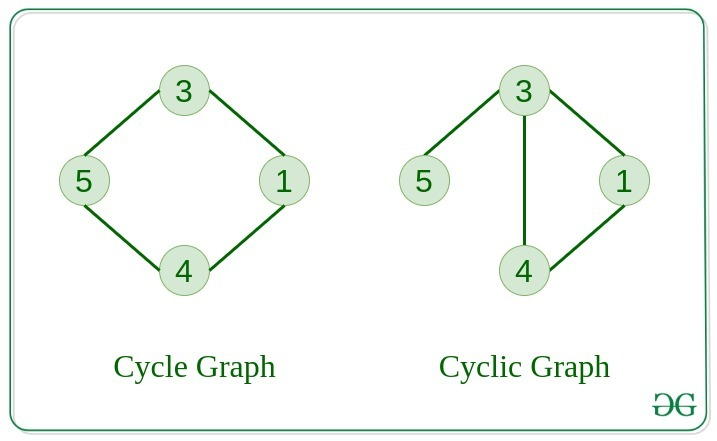
- 연결 그래프 (Connected Graph) vs 비연결 그래프 (Disconnected Graph)
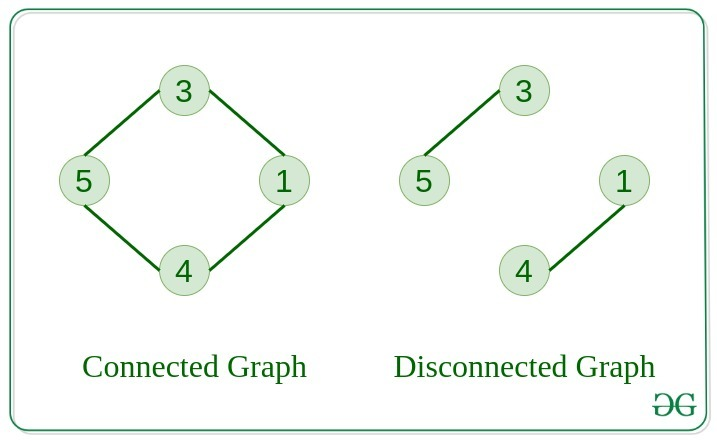
- 완전 그래프 (Complete Graph)
- 모든 노드 간에 간선이 존재하는 그래프
- 모든 노드가 서로 연결되어 있는 상태입니다.
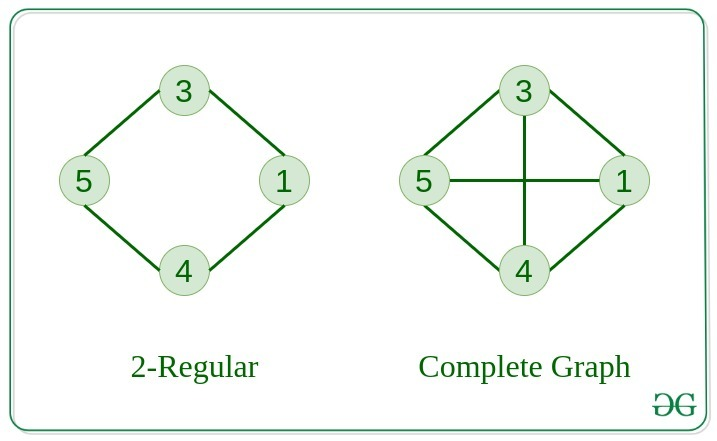
💋 트리 구조 vs 그래프 구조
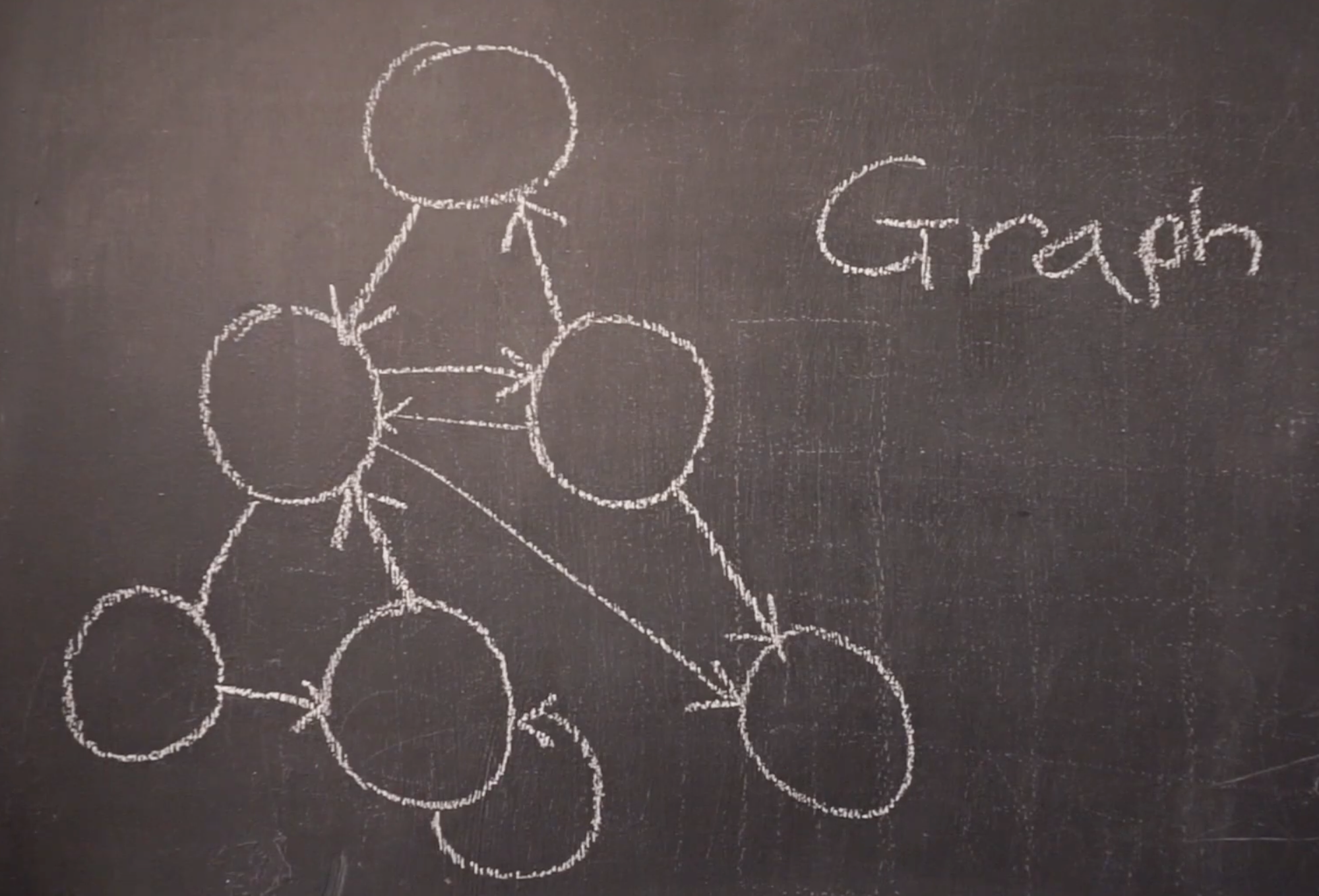
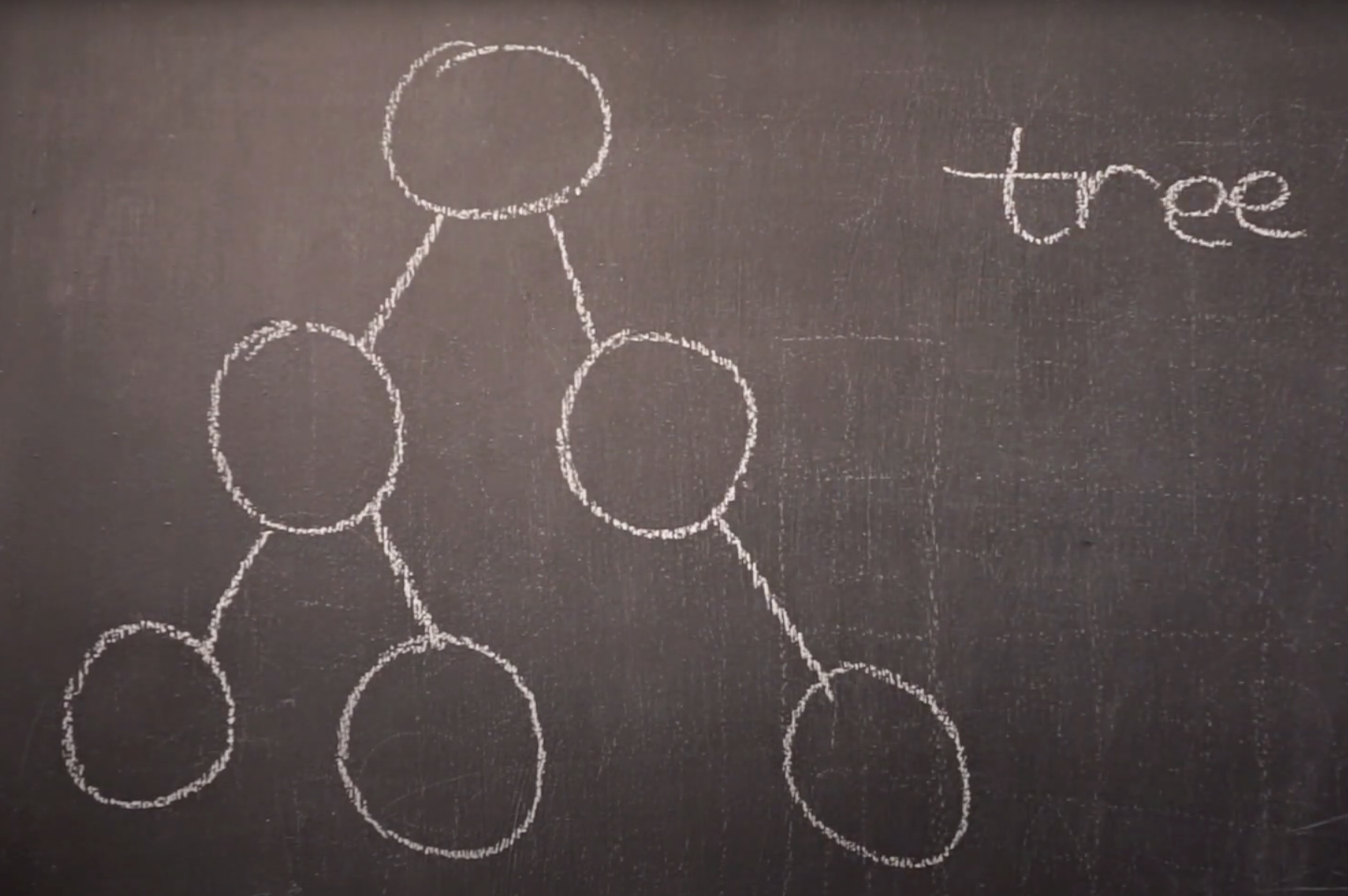
이전에 학습한 트리의 특징은 다음과 같았다.
- 루트 노드는 딱 1개만 존재한다.
- 트리 내에 사이클은 존재하지 않는다.
- 자녀 노드는 하나의 부모 노드만 가진다.
- 데이터를 순차적으로 저장하지 않는 비선형 구조
- 트리에 서브 트리가 있는 재귀적 구조
- 계층적 구조
트리구조랑 딱 비교해서 그래프 자료구조의 특징은 다음과 같다.
- 그래프에서는 모든 노드가 동등하게 취급되며, 루트 노드의 개념이 없다.
- 그래프 자료구조는 사이클이 존재할 수도 있다.
- 사이클의 방향이 자유로워서, 부모 자녀 노드의 개념이 없다.
- 데이터를 순차적으로 저장하지 않는 비선형 구조 ⇒ 트리와 동일
- 그래프에 서브 그래프가 있는 재귀적 구조 ⇒ 트리와 유사함
- 계층적 X
⇒ 그래프 자료구조를 일반화된 트리라고도 볼 수 있다.
Trees are the restricted types of graphs, just with some more rules. Every tree will always be a graph but not all graphs will be trees. Linked List, Trees, and Heaps all are special cases of graphs. - geeksforgeeks
💋 Graph를 표현하는 방법
✔️ Adjacency Matrix
- 그래프를
2차원 배열로 나타내는 방법 - 연결되었으면 1, 연결되지 않았으면 0으로 나타낸다.
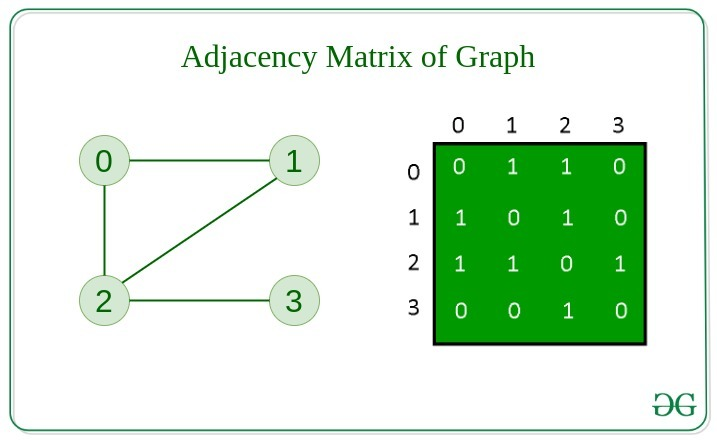
- 가중치 그래프인 경우에는 각 원소가 가중치 값을 나타낼 수 있다.
- 간선의 존재 여부를 상수 시간에 확인할 수 있지만, 간선의 수가 상대적으로 매우 적은 경우(희소한 그래프) 많은 메모리를 차지할 수 있다. ⇒ 그냥 의미없는 0으로 가득 채워진 배열…!
✔️ Adjacency List
- 각 노드마다 인접한 노드들을 LinkedList로 나타내는 방법
- 전체 노드의 2배에 해당하는 양의 데이터를 저장해야 한다. (연결은 서로 되는거니깐 2배임)
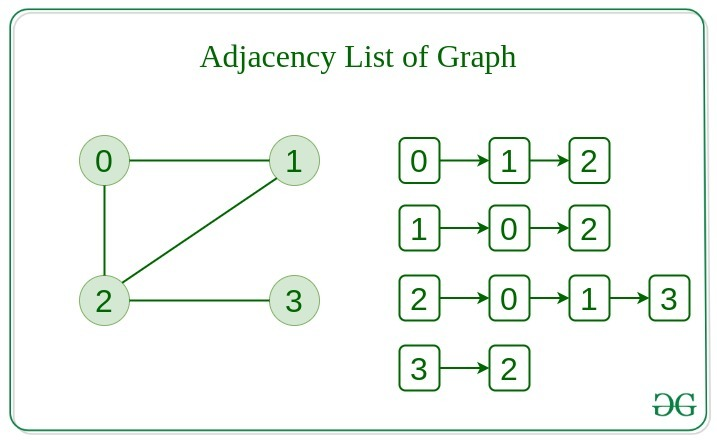
- 가중치 그래프인 경우에는 가중치 값도 함께 저장될 수 있다.
- 간선의 수가 상대적으로 매우 적은 경우(희소한 그래프)에도 메모리를 효율적으로 사용할 수 있다.
- 간선의 존재 여부를 확인하려면 해당 노드의 연결 리스트를 순회해야 한다.
💋 참고자료
- https://www.geeksforgeeks.org/introduction-to-graphs-data-structure-and-algorithm-tutorials/
- https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/
- https://www.youtube.com/watch?v=fVcKN42YXXI

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
반응형