[Algorithm] 시간 복잡도(Time Complexity)란?
Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS
GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip
주니어 개발자를 위한 전공 지식 모음.zip. Contribute to seoul-developer/CS development by creating an account on GitHub.
github.com
이 포스팅은 유튜버 쉬운코드님의 시간 복잡도 영상을 보고 작성했습니다.
💋 시간 복잡도
✔️ 개념
코드의 실행 시간이 어느 정도인지 표현하기 위해 만들어진 개념이다.
실제 실행 시간은 CPU 성능에 따라 달라지기 때문에, 실행 시간을 측정하는 대신 연산의 실행 횟수를 카운트한다.
⇒ 시간 복잡도는 입력의 크기에 따른 알고리즘 수행에 필요한 step 수로 측정한다.
(실제 실행 시간은 대강 1초에 1억번 연산이라고 생각하면 된다.)
✔️ 계산 방법
각 라인을 실행하는데 들어가는 시간(비용)이 있을 텐데, 그걸 각각 c1 ~ c4라고 하고 각 라인이 몇 번씩 실행되는지를 세어 보았다. (반복문은 전부 실행되었나 체크하는 횟수도 한 번 있어서 N+1이다.)
실행 횟수는 inputs의 사이즈를 N이라고 했을 때, 입력 크기에 따른 알고리즘 수행에 필요한 step 수이다.

최종적으로 실행 시간은 각각 라인의 비용과 실행 횟수를 곱한 것의 합이다.
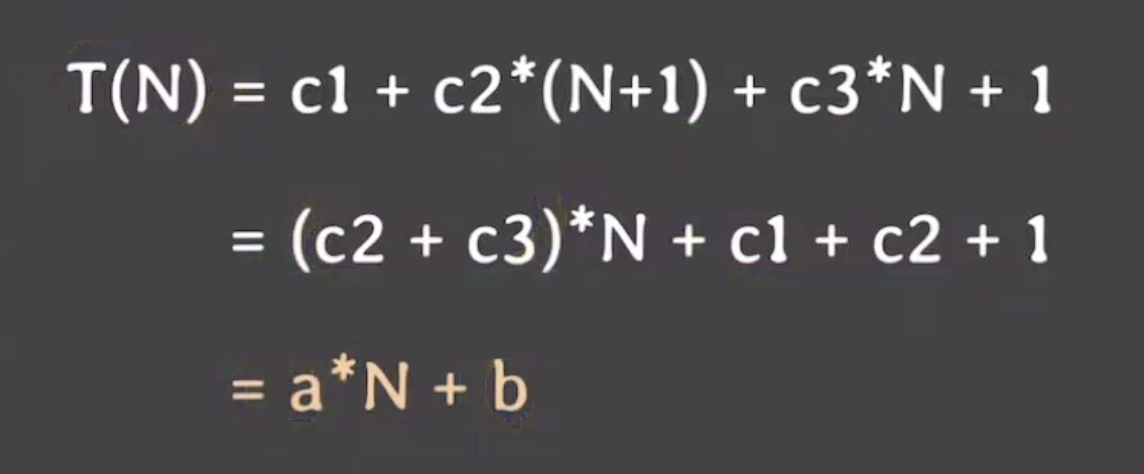
이렇게 계산한 것보다 더 정확한 계산은 하기 어렵다.
또, N이 작을 때 실행 시간은 굳이 계산해볼 필요도 없다. 우리가 중요한 것은 N이 점점 커져서 무한대로 수렴할 때!
N이 커질 수록 a * N + b 에서,
- 최고 차항만 의미있다. ⇒
a * N만 중요함 - 최고 차항의 계수는 의미 없다. ⇒ N만 중요함

✔️ 점근적 분석 (Asymptotic Analysis)
데이터의 개수 n→∞일때 어떤 함수 형태에 근접해지는지 분석하는 방법이다.
유일한 분석법도 아니고 가장 좋은 분석법도 아니지만, 그나마 가장 간단하고 실행시간을 단순하게 표현할 수 있어서 많이 사용되고 있다.
⇒ 시간 복잡도는, 함수의 실행 시간은 점근적 표기법으로 표현하는 것!
💋 시간 복잡도의 표기법
✔️ 시간 복잡도의 하한선 vs 상한선
같은 함수라도 데이터의 구조나 분포에 따라서 실행 시간이 달라질 수 있다.

이렇게, 문장으로 함수 실행 시간의 하한선과 상한선을 나타낼 수 있다.

위와 같은 문장을 기호로 나타내면 다음과 같다.
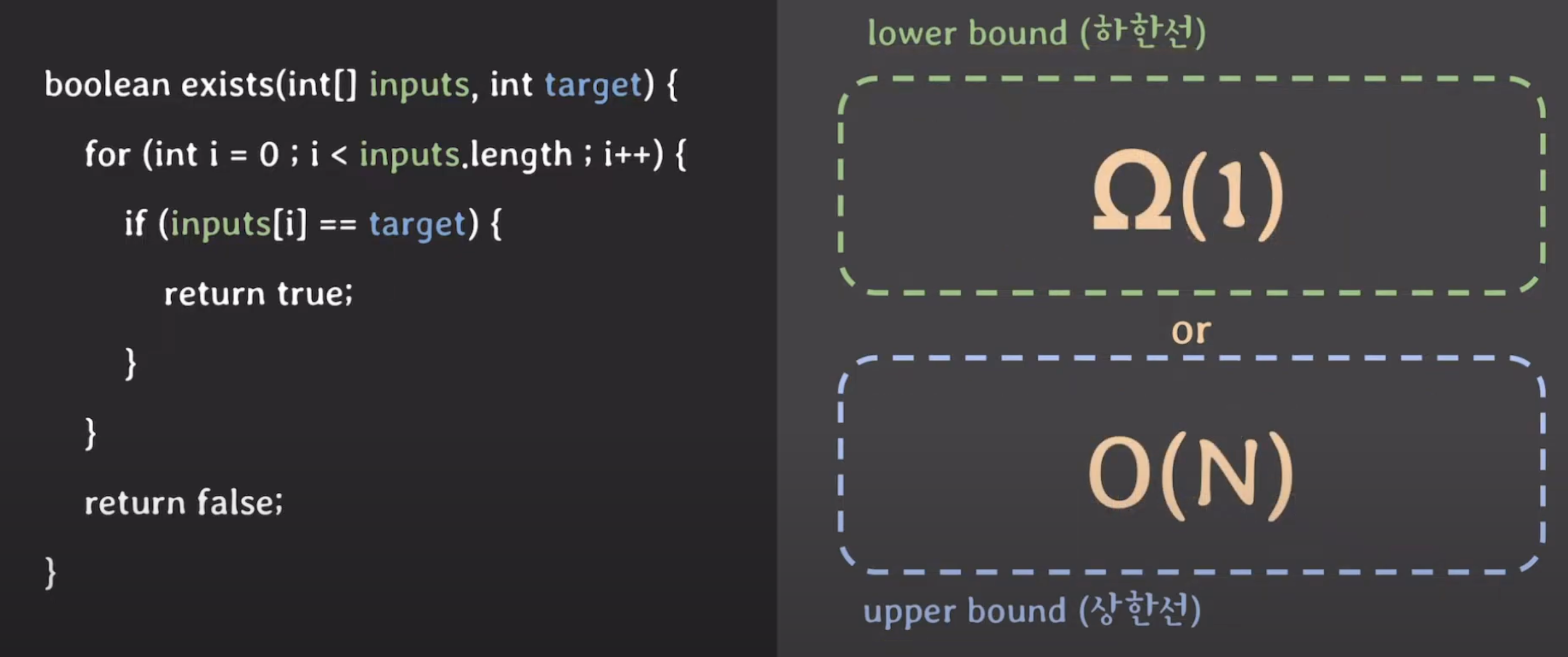
✔️ 표기법
시간 복잡도의 하한과 상한을 표현하는 데는 빅-오(O), 빅-오메가(Ω), 빅세타(Θ) 등의 기호가 사용된다.
- 빅-오(O) ⇒ 상한선(upper bound)
- 빅-오메가(Ω) ⇒ 하한선(lower bound)
- 빅-세타(Θ) ⇒ 평균적인 경우(average case)
시간 복잡도를 고려하는 것은 상한선을 중요하게 생각하는 것이기 때문에, 주로 빅-오(O) 표기법이 많이 사용된다.

상한선과 하한선이 같은 경우에 lower bound, upper bound가 아주 가까이 있다는 의미로 tight bound라고도 한다. 이 경우, 빅-세타(Θ)로 표기할 수 있다. 예를 들어, 어떤 함수가 Θ(N)의 시간 복잡도를 가진다면, 그 케이스에서 상한과 하한 모두 선형 시간 복잡도를 가진다고 알려주는 것이랑 동일하다.
✔️ 점근적 표기법 vs case 분류
각 케이스 별로 점근적 표기법을 모두 사용해서 상한, 하한, 평균을 나타낼 수 있다.

💋 이진 탐색의 시간 복잡도
✔️ 이진 탐색이란?
이진 탐색(Binary Search)은 정렬된 배열에서 원하는 값을 빠르게 찾기 위한 알고리즘이다.
주어진 배열에서 중간 값과 비교하여 찾고자 하는 값이 중간 값보다 작으면 배열의 왼쪽 반을, 크면 오른쪽 반을 선택하여 탐색을 반복한다.
위 과정을 반복하여 찾고자 하는 값을 찾거나, 배열의 범위가 축소되어 더 이상 나눌 수 없을 때까지 반복한다.
✔️ Worst Case
이진 탐색의 worst case 시간 복잡도에 대해 알아보자!

이진 탐색은 한 번 실행할 때마다 탐색하는 범위가 1/2씩 사이즈가 줄어든다.
worst case의 경우에는, 찾는 값이 없을 때이다. 배열의 범위가 1까지 축소되어 찾는 값이 없다는 것을 확인할 때까지 실행해야 하는데, 몇 번을 실행해야 사이즈가 1이 될까?
input size를 N이라고 했을 때, k번 실행했을 때 사이즈가 1이 되어 탐색이 종료될 것이라고 해보자.
N * (1/2)^k = 1
N = 2^k
k = log2N
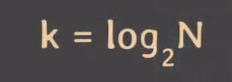
근데 이걸 점근적 표기법으로 표기하면,

✔️ Best Case
best case는 한 번에 찾았을 때다. 찾으려는 숫자가 정중앙에 있을 때이고, 이 경우의 시간 복잡도는 Θ(1)이다.
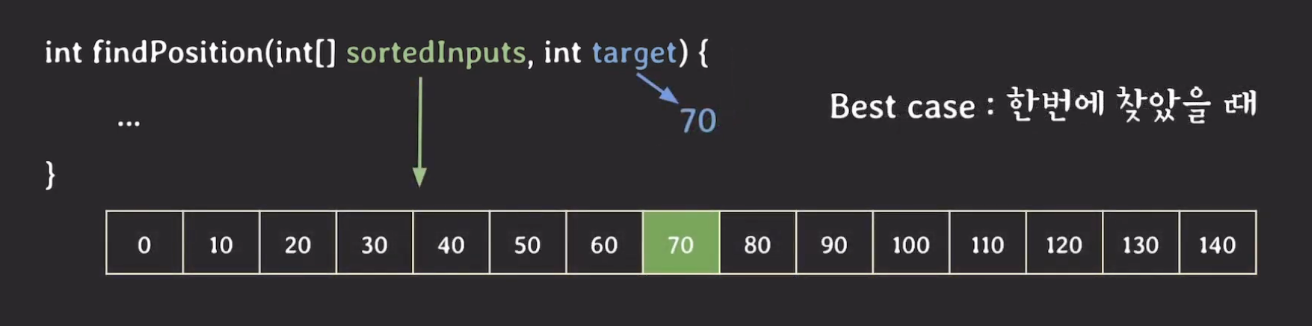
✔️ 시간 복잡도
이진 탐색의 케이스 별 시간 복잡도를 정리하면 아래와 같다.

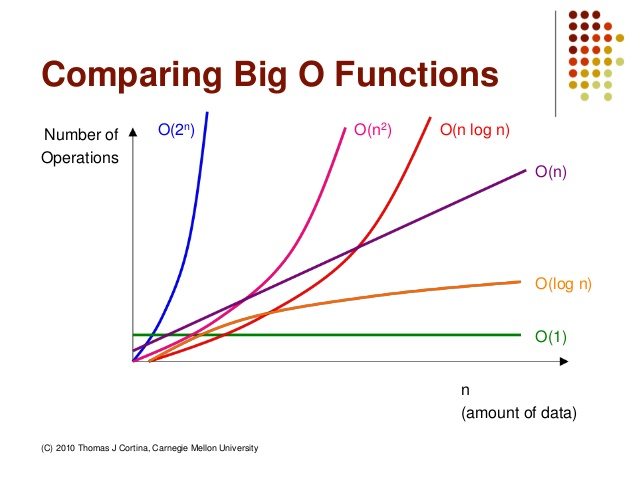
💋 시간 복잡도 속도 비교
오른쪽으로 갈수록 느려지고, 성능이 안좋아진다.
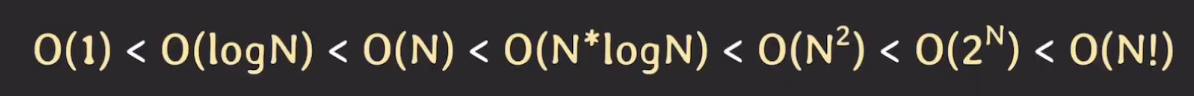
💋 예제



💋 참고자료
- https://www.youtube.com/watch?v=tTFoClBZutw
- http://contents2.kocw.or.kr/KOCW/document/2015/pukyong/kwonoeum/1.pdf
- https://www.codeit.kr/community/questions/UXVlc3Rpb246NWViMjFmNDMwZWE4YjUwNmEyMDlhYTAx

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!