🌏 차등 프라이버시 (ε-Differential Privacy)
데이터셋 D=(x1,x2,…,xn) 이 있고, 이로부터 어떤 통계값 f(D)를 공개하고 싶다고 가정합니다. 그런데 직접 f(D)f(D)를 공개하면 개인정보가 유출될 수 있기 때문에, 노이즈를 섞는 방법(무작위화, randomization)을 사용합니다.
✅ Neighboring dataset
D와D′는 단 한 사람의 데이터만 다른 데이터셋이라고 가정합니다. 아래와 같이 n번 데이터 하나만 다르고 1~n-1 의 데이터는 모두 같습니다.
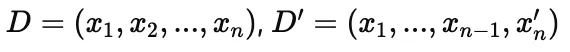
- 이 둘을 neighboring datasets라고 부릅니다.
✅ DP의 수식적 정의
어떤 메커니즘 M이 다음을 만족하면, 이를 ε-차등 프라이버시라고 부릅니다.
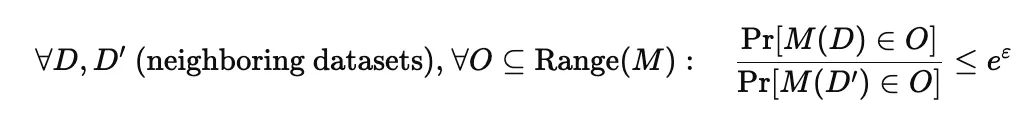
- ε은 프라이버시 손실 허용 정도를 의미하는 파라미터입니다.
- 작을수록 더 높은 프라이버시 보장
M(D)은 노이즈를 섞은 통계값을 의미합니다. (예:f(D)+Z)
✅ O는 "출력값의 집합"
여기서 O는 무작위 메커니즘 MM의 출력값 중 어떤 특정한 "결과 집합"을 의미해요.
"메커니즘 M의 출력이 이 집합 O에 속할 확률"을 나타냅니다.
예를 들어서, M(D)는 "평균 키"를 출력하는 메커니즘이고, 그 값에 라플라스 노이즈가 섞여 있다고 해봅시다.

"노이즈가 섞였을 때, 결과가 168cm~172cm 사이에 나올 확률은 얼마일까?"
이런 경우, O=[168,172] 라고 두고,
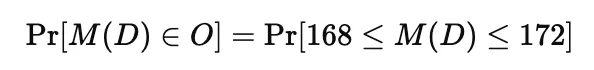
이렇게 생각하면 됩니다.
차등 프라이버시의 핵심은 "어떤 결과 집합이든, 그 안에 결과가 들어갈 확률이 두 이웃 데이터셋 D, D'에서 크게 다르지 않아야 한다"는 것입니다.
- 즉,
누군가의 데이터가 바뀌었다고 해서 어떤 특정한 결과 집합에 포함될 확률이 급격히 달라지면 안 됩니다. - 그래서 모든 가능한 출력 집합 O에 대해 이 확률 비율을 제한합니다

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
'Computer Science > Data Privacy' 카테고리의 다른 글
| [Data Privacy] Reconstruction Attack: 재구성 공격이란? 랜덤을 사용해 가장 쉽게 막는 방법 (0) | 2025.03.27 |
|---|
🌏 차등 프라이버시 (ε-Differential Privacy)
데이터셋 D=(x1,x2,…,xn) 이 있고, 이로부터 어떤 통계값 f(D)를 공개하고 싶다고 가정합니다. 그런데 직접 f(D)f(D)를 공개하면 개인정보가 유출될 수 있기 때문에, 노이즈를 섞는 방법(무작위화, randomization)을 사용합니다.
✅ Neighboring dataset
D와D′는 단 한 사람의 데이터만 다른 데이터셋이라고 가정합니다. 아래와 같이 n번 데이터 하나만 다르고 1~n-1 의 데이터는 모두 같습니다.
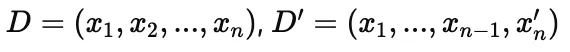
- 이 둘을 neighboring datasets라고 부릅니다.
✅ DP의 수식적 정의
어떤 메커니즘 M이 다음을 만족하면, 이를 ε-차등 프라이버시라고 부릅니다.
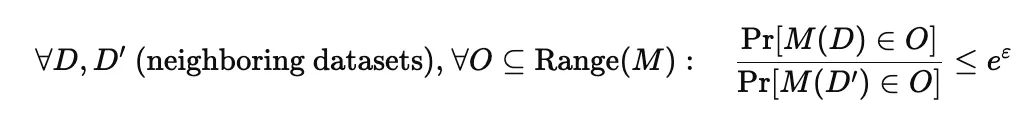
- ε은 프라이버시 손실 허용 정도를 의미하는 파라미터입니다.
- 작을수록 더 높은 프라이버시 보장
M(D)은 노이즈를 섞은 통계값을 의미합니다. (예:f(D)+Z)
✅ O는 "출력값의 집합"
여기서 O는 무작위 메커니즘 MM의 출력값 중 어떤 특정한 "결과 집합"을 의미해요.
"메커니즘 M의 출력이 이 집합 O에 속할 확률"을 나타냅니다.
예를 들어서, M(D)는 "평균 키"를 출력하는 메커니즘이고, 그 값에 라플라스 노이즈가 섞여 있다고 해봅시다.

"노이즈가 섞였을 때, 결과가 168cm~172cm 사이에 나올 확률은 얼마일까?"
이런 경우, O=[168,172] 라고 두고,
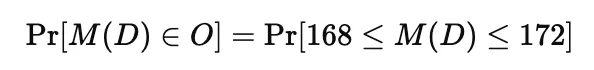
이렇게 생각하면 됩니다.
차등 프라이버시의 핵심은 "어떤 결과 집합이든, 그 안에 결과가 들어갈 확률이 두 이웃 데이터셋 D, D'에서 크게 다르지 않아야 한다"는 것입니다.
- 즉,
누군가의 데이터가 바뀌었다고 해서 어떤 특정한 결과 집합에 포함될 확률이 급격히 달라지면 안 됩니다. - 그래서 모든 가능한 출력 집합 O에 대해 이 확률 비율을 제한합니다

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
'Computer Science > Data Privacy' 카테고리의 다른 글
| [Data Privacy] Reconstruction Attack: 재구성 공격이란? 랜덤을 사용해 가장 쉽게 막는 방법 (0) | 2025.03.27 |
|---|
