🌍 퍼셉트론(Perceptron)
딥러닝의 시작은 “하나의 뉴런을 수학적으로 흉내 낸 것”으로 이것을 퍼셉트론(Perceptron) 이라고 부릅니다.
퍼셉트론은 입력을 받아 → 가중치를 곱하고 → 합친 뒤 → 결과를 출력하는 단순한 모델이에요.
이 기본 단위가 여러 개 연결되면, 우리가 알고 있는 신경망(Neural Network) 이 됩니다.
✅ Perceptron
하나의 퍼셉트론은 아래와 같습니다.
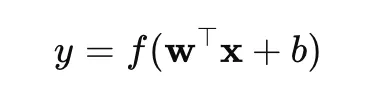
- x : 입력 (예: 픽셀 값, 데이터 피처)
- W : 가중치 matrix (입력마다 중요도를 조절, 직접 정하는게 아니라 학습을 통해 자동으로 조절됨!!!)
- b : 바이어스 (기울기 조정용 상수)
- f(·) : 활성화 함수 (activation function, 예: sigmoid, ReLU 등)
입력이 많을수록, 퍼셉트론이 여러 특징(feature) 을 조합해서 판단합니다.
[한계] 퍼셉트론은 선형 분리 가능한 데이터만 학습 가능하다는 한계가 있습니다. 즉 저 1차 식 wx+b를 바탕으로 위인지 아래인지 둘중 하나로만 가를 수 있기 때문에 선형 경계만 표현할 수 있습니다 (= 즉, 단일 퍼셉트론으로는 XOR 문제처럼 비선형 경계를 표현할 수 없습니다.)
이 한계를 극복하기 위해 다층 퍼셉트론(Multi-Layer Perceptron, MLP) 이 등장합니다.
✅ Multi Layer Perceptron (MLP)
퍼셉트론이 여러 개 모이면 다층 퍼셉트론(MLP: Multi-Layer Perceptron) 이 됩니다.
Input Layer → Hidden Layer(s) → Output Layer- 입력층(Input layer) : 데이터가 처음 들어오는 곳
- 은닉층(Hidden layer) : 가중치·활성화 함수를 통해 특징을 추출
- 출력층(Output layer) : 최종 예측 결과 (예. “고양이”, “강아지”, 1.25와 같은 연속적인 숫자)
MLP는 은닉층(hidden layer)에 비선형 활성화 함수를 추가하여 복잡한 패턴을 학습합니다.
딥러닝이 “Deep”한 이유는 바로 은닉층이 깊게 여러 층 쌓여 있기 때문입니당
각 층이 데이터의 더 복잡한 패턴을 학습하면서, 모델의 표현력이 강해집니다.
🌍 손실 함수, 역전파(Backpropagation), 옵티마이저
신경망은 “정답을 얼마나 잘 맞추는가”를 계속 확인하면서 가중치를 조금씩 조정합니다.
이때 얼마나 잘 맞추는가의 판단에 손실함수가 사용됩니다.
✅ 손실 함수 (Loss Function)
모델의 “예측이 얼마나 틀렸는지”를 수치로 계산하는 함수예요.

여러 가지 손실함수가 있지만 그중에서도 특히 2가지가 유명한데, MSE와 CEL입니다.
- MSE (Mean Squared Error) : 회귀 문제에 사용
- Cross Entropy Loss : 분류 문제에 사용
분류 문제에서는 Cross Entropy Loss를 주로 사용하며,
이때 모델의 출력층은 Softmax 함수를 통해 각 클래스 확률을 산출합니다.
Cross Entropy는 이 확률 분포와 정답(one-hot 벡터)의 차이를 계산합니다.
✅ 역전파 (Backpropagation)
손실이 생겼다면, 그 손실이 어디서 얼마나 생겼는지를 추적해서 가중치를 수정해야 하는데, 그걸 수학적으로 처리하는 과정이 역전파(Backpropagation) 입니다.
출력층에서 생긴 오차를 거꾸로 전파(backpropagate)하면서
각 가중치가 얼마나 잘못되었는지 계산하는 과정
이때 미분(∂)을 이용해서 기울기(gradient) 를 구하고, 그걸로 어느 방향으로 가중치를 바꿔야 손실이 줄어드는지 판단합니다.
위에서 언급했던 거처럼 W(가중치) 는 사람이 직접 지정하지 않고, 손실함수–역전파–옵티마이저 과정을 통해 자동으로 학습됩니다.
✅ 옵티마이저 (Optimizer)
역전파로 구한 기울기를 이용해서, 가중치를 실제로 업데이트하는 알고리즘입니다.
가장 기본적인 건 경사하강법(Gradient Descent)입니다.

- η (Eta) : 학습률(learning rate)로, 얼마나 크게 한 번에 움직일지 결정하는 파라미터
- 크게 잡으면 빨리 최적점에 닿을 수도 있지만 영원히 닿지 못하고 횡보할 수도 있습니다.
- 작게 잡으면 정말 느리게 최적점에 가기 때문에 적절한 값을 설정해주어야 합니다.
- ∂L/∂W : 손실에 대한 가중치의 기울기
AI 개발에서 모델이 학습을 통해 자동 조정하는 값(W, b) 들을 파라미터(parameter) 라고 합니다.
반면, 개발자가 직접 설정하는 값(learning rate, epoch, batch size, optimizer 등) 은 하이퍼파라미터(hyperparameter) 라고 구분합니다.
옵티마이저 관련해서 많은 하이퍼 파라미터들이 등장합니다. 우선 위에서 나온 학습률도 직접 정해야 하고, 기울기는 계산에 따라 정해지지만 이때 사용되는 옵티마이저의 종류도 직접 정해야 합니다. Optimizer는 기울기를 얼마나, 어떻게 반영할지를 다르게 설계한 버전들이 많습니당
| Optimizer | 특징 | 사용 사례 |
|---|---|---|
| SGD | 일반화 성능이 좋음, 단 수렴 느림 | 정제된 대규모 데이터 |
| Adam | 학습률 자동 조정, 빠른 수렴 | 실험적, 초기 탐색 단계 |
| AdamW | Weight Decay를 분리, 과적합 방지 | 고성능 모델 파인튜닝 |
| - RMSProp, Adagrad : 특정 상황에 강한 변형들 |
🌍 DL 개발의 흐름
DL 개발의 큰흐름은 아래와 같습니다. Epoch 수 만큼 반복해서 학습을 하게 됩니다. (파라미터에 따라 중간에 멈출지 등등을 세밀하게 조정할 수 있습니다)
[입력 데이터]
↓
[신경망 Forward] → 예측
↓
[손실 함수 계산]
↓
[Backpropagation: 기울기 계산]
↓
[Optimizer로 가중치 업데이트]
↓
[다음 Epoch 학습 반복]🌍 Perceptron in torch
✅ Forward Perceptron
# 모델 정의
import torch
import torch.nn as nn
class MLP(nn.Module):
def __init__(self):
super().__init__()
# 입력 10 → 은닉 32 → 출력 2 (분류 문제 가정)
self.fc1 = nn.Linear(10, 32)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
x = self.fc1(x) # Wx + b
x = self.relu(x) # 활성화 함수 f()
x = self.fc2(x) # Output layer
return x
model = MLP()fc1,fc2→ 퍼셉트론 / MLP의 층(layer)ReLU()→ 활성화 함수forward()→ 신경망 Forward 연산 (Wx+b → f → 출력)
✅ 손실 함수 (Loss Function)
criterion = nn.CrossEntropyLoss() # 분류 문제용 손실 함수criterion= 손실 함수 L(y, ŷ)- “모델의 예측값과 정답(label)의 차이”를 계산하는 역할
- 회귀라면
nn.MSELoss()사용
✅ 역전파 (Backpropagation)
loss = criterion(outputs, labels) # 손실 계산
loss.backward() # 역전파 수행 (∂L/∂W 계산)loss.backward()→ Backpropagation 실행 부분- 내부적으로 PyTorch가 자동 미분(autograd) 으로 기울기를 계산합니다.
- 여기서 계산된 기울기는 각 파라미터(
W,b)에 저장됩니다.
✅ 옵티마이저 (Optimizer)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
optimizer.zero_grad() # 이전 기울기 초기화
loss.backward() # 새로운 기울기 계산
optimizer.step() # 가중치 업데이트optimizer→ 경사하강법 알고리즘 (SGD, Adam 등)zero_grad()→ 이전 iteration의 gradient를 초기화step()→ 가중치 업데이트 (( W = W - \eta \cdot ∂L/∂W ))
✅ 학습 루프
for epoch in range(num_epochs):
for inputs, labels in dataloader:
outputs = model(inputs) # [1] Forward
loss = criterion(outputs, labels) # [2] 손실 계산
optimizer.zero_grad() # [3] 기울기 초기화
loss.backward() # [4] 역전파
optimizer.step() # [5] 옵티마이저 업데이트
print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
| 코드 | 이론 대응 | 설명 |
|---|---|---|
model(inputs) |
Forward | 신경망 계산 (Wx+b → f) |
criterion(...) |
Loss Function | 예측 오차 계산 |
loss.backward() |
Backpropagation | 기울기 계산 |
optimizer.step() |
Optimizer | 가중치 갱신 |
반복(for epoch) |
학습 루프 | 여러 번 학습 (Epoch) 반복 |

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
'AI > 딥러닝' 카테고리의 다른 글
| [AI/DL] 딥러닝의 발전(2): RNN에서 Transformer까지 — 순차 데이터와 Self-Attention 이해하기 (0) | 2025.10.20 |
|---|---|
| [AI/DL] 딥러닝의 발전(1): AlexNet, ResNet, YOLO (2012~2016) (0) | 2025.10.17 |
| [AI/DL] GAN(Generative Adversarial Networks): Generator vs Discriminator 의 경쟁적인 가짜 찾아내기 (0) | 2024.12.06 |
| [AI/DL] Convolutional Neural Networks(CNN)에서 합성곱 연산과 파라미터 계산 (0) | 2024.10.24 |
| [AI/DL] CNN의 등장 배경: 공간 정보를 활용하며 단계적으로 학습하기 (1) | 2024.10.23 |
