Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS
GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip
주니어 개발자를 위한 전공 지식 모음.zip. Contribute to seoul-developer/CS development by creating an account on GitHub.
github.com
💋 DB 인덱스가 B-Tree 자료구조를 사용하는 이유
데이터베이스의 인덱스는 B-Tree 자료구조를 사용한다.
✔️ 시간 복잡도

- B-Tree 계열의 B+Tree, B*Tree
- 균형 트리이기 때문에 평균과 최악의 경우 모두
O(logN)의 시간 복잡도를 가진다. - 이진 탐색 트리
- 균형이 얼추 맞는 경우
O(logN)의 시간 복잡도를 가진다. - 변질 이진 트리의 형태에 가까운 경우
O(n)의 시간 복잡도를 가진다 - Self-Balancing 이진 탐색 트리의 종류인 AVL Tree와 Red-Black 트리
- 스스로 균형을 맞춰, 모든 경우에
O(logN)의 시간 복잡도를 가진다.
- Hash Index
- 삽입/삭제/조회 시간 복잡도가
O(1)이다. - 하지만,
equality(=)조회만 가능하고, 범위 기반 정렬에는 사용될 수 없다.
⇒ 고려하지 않음
시간 복잡도에 큰 차이가 없는데, 왜 self-balancing BST가 아니라 B-Tree를 사용하는걸까?
✔️ 컴퓨터 시스템 구성


- CPU
- 프로그램 코드가 실제로 실행되는 곳
- 메인 메모리(RAM)
- 실행중인 프로그램의 코드, 코드 실행에 필요한 데이터들이 상주하는 곳
- 용량이 작아서, 여기에 다 담지 못하는 데이터 중 자주 사용하지 않는 메모리 중 일부는 SSD에 저장한다 ⇒ Swap 메모리라고 한다
휘발성메모리로, 전원이 켜진 동안에만 데이터를 저장할 수 있다.- secondary memory보다 데이터 처리 속도가 빠르다(
0 ~ 50GB/s) - secondary storage(SSD or HDD)
- 프로그램과 데이터가
영구적으로 저장되는 곳 ⇒ 껐다 켜도 남아있다! - 실행중인 프로그램의 데이터 일부가 임시 저장 되는 곳
- 데이터 처리 속도가 가장 느리다. (SSD:
3 ~ 5 GB/s, HDD:0.2 ~ 0.3GB/s) - block 단위로 데이터를 읽고 쓴다.
- block은 파일 시스템이 데이터를 읽고 쓰는 논리적 단위
- block의 크기는 대표적으로 4KB, 8KB, 16KB 등이 있다.
- 불필요한 데이터까지 읽어올 가능성이 있다. ⇒ 비효율
- 데이터베이스가 이곳에 저장된다!
영구적으로 저장되어야 하기 때문!- 데이터의 사이즈가 매우 크고, 계속해서 사이즈가 늘어나기 때문!
✔️ 데이터베이스의 성능을 높이는 방법

- 데이터베이스에서 데이터를 조회할 때, secondary storage에
최대한 적게 접근하는 것이 성능 면에서 좋다! - block 단위로 읽고 쓰기 때문에,
연관된 데이터를 모아서 저장하면 더 효율적으로 읽고 쓸 수 있다.
'
✔️ AVL Tree vs B-Tree로 인덱스 만들기
(Red-Black 트리의 경우에도 결과는 AVL 트리와 유사하다.)
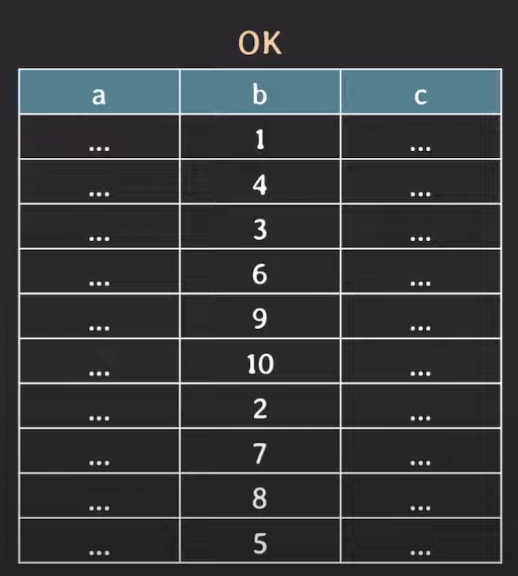
위의 테이블에 대해서 b에 대해서 인덱스를 생성하려고 한다.
CREATE INDEX(b)
- 가정
- 트리의 각 노드는 서로 다른 block에 있다.
- 초기의 루트 노드를 제외한 모든 노드는 secondary storage에 있다.
- 초기에는 데이터 자체도 모두 secondary storage에 있다.
AVL tree index(b)

b = 5인 데이터를 찾는다고 할 때, secondary storage에서 6, 3, 4의 포인터를 거쳐 5를 찾아내고, 5가 저장된 위치를 알아내 테이블에 접근한다.
⇒ AVL Tree index는 Secondary Storage에 4번 접근
5차 B Tree index(b)
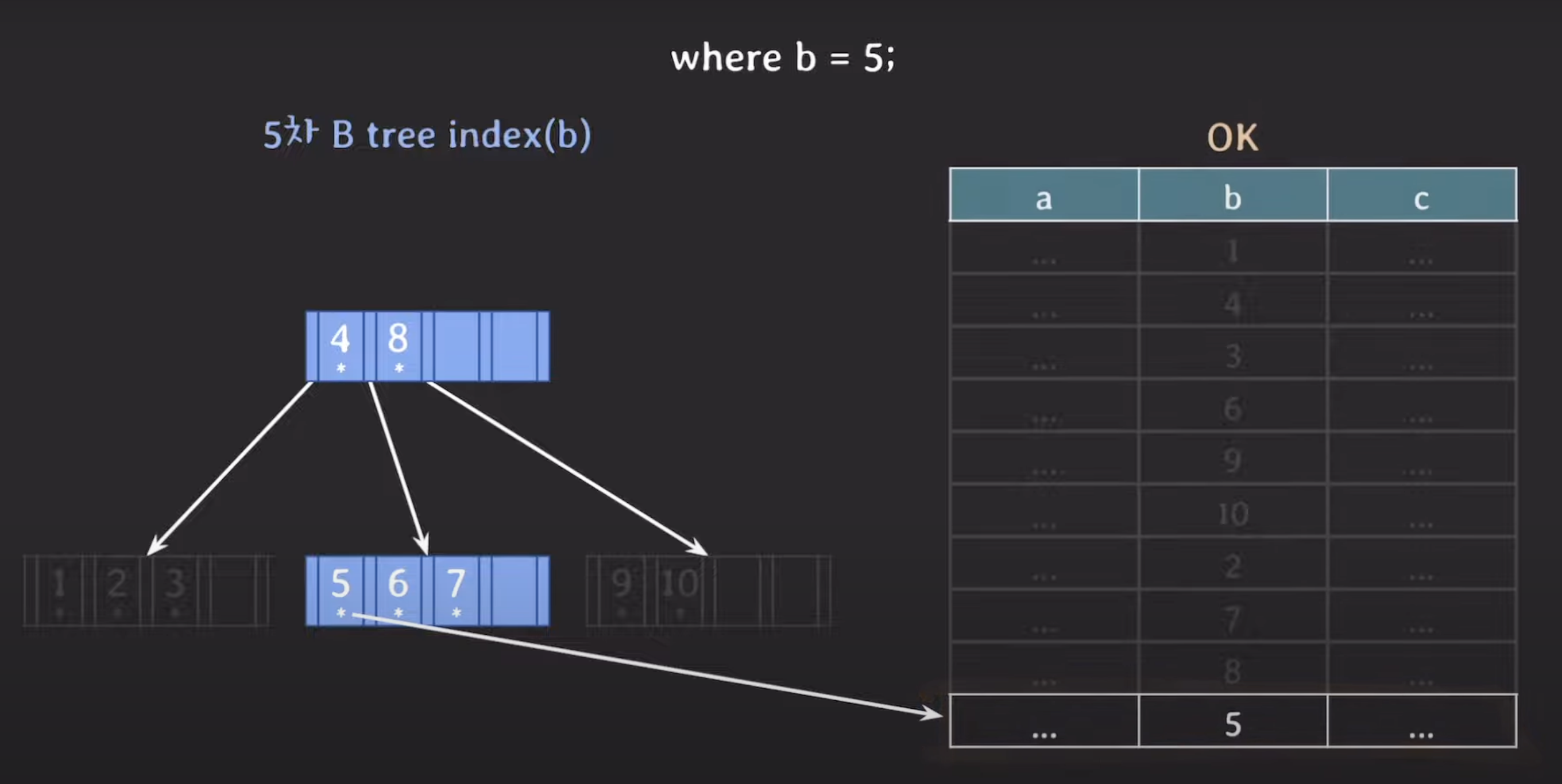
⇒ 5차 B Tree index는 Secondary Storage에 2번 접근
✔️ 결과
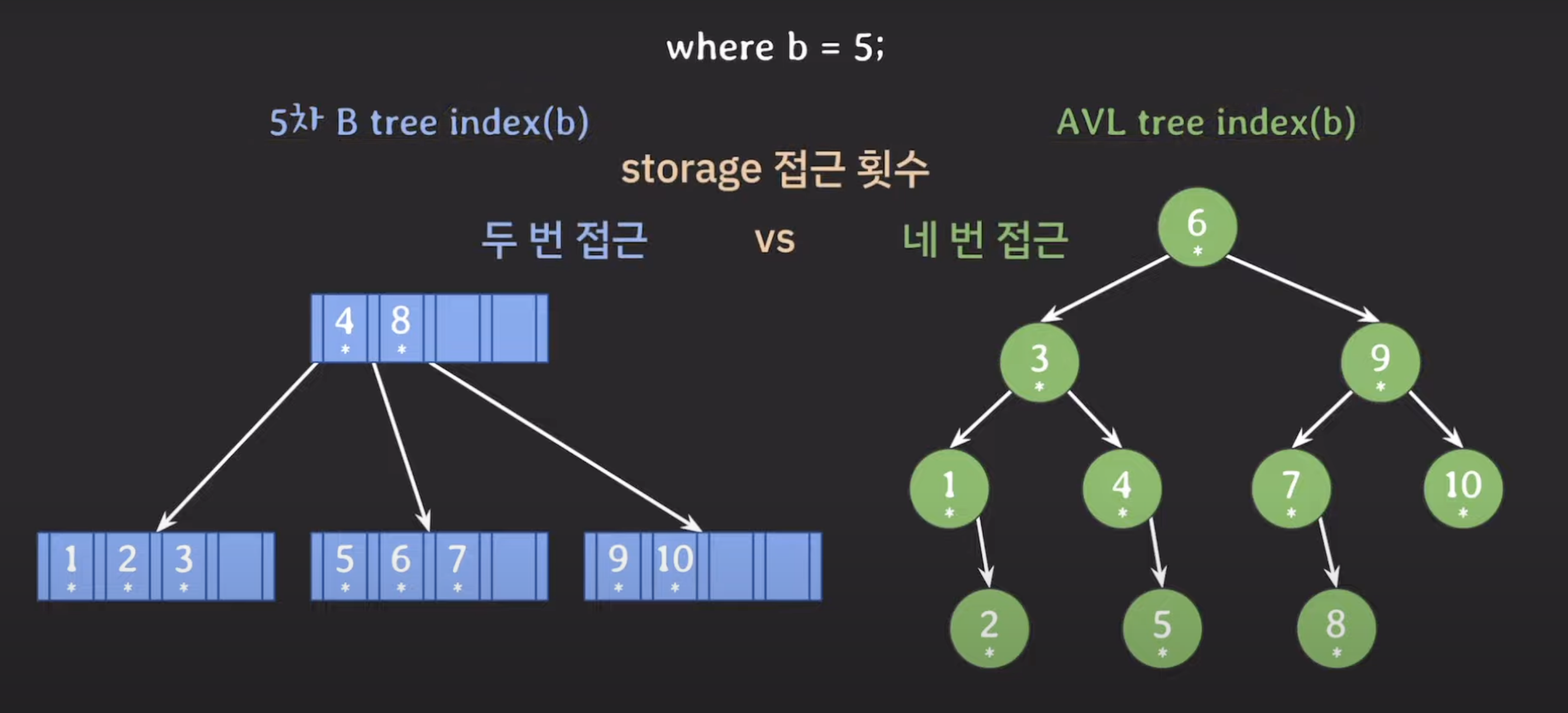
Secondary Storage에 접근하는 작업이 오래 걸리는데, B Tree를 사용한 인덱스에서는 접근 횟수가 훨씬 적게 나타난다.
B Tree는 자녀 노드의 수를 여러 개 가질 수 있지만, AVL Tree는 자녀 노드를 2개 이하로만 가질 수 있다. 따라서, B Tree는 데이터를 찾을 때, 탐색 범위를 더 빠르게 좁혀 나갈 수 있다. (루트 노드에서 리프 노드까지의 거리가 짧아진다.)
⇒ B Tree의 성능이 우수하다.

또 하나의 노드에 있는 데이터 수로 비교했을 때, 5차 B Tree는 2~4개고, AVL Tree는 1개다. block 단위로 가져오게 될 때, AVL Tree는 하나의 데이터와 함께 블락의 나머지 공간에는 관련 없는 데이터를 가져오게 되는 반면, B Tree는 실제로 사용될 데이터를 함께 가져올 가능성이 높다.
⇒ Block 단위에 대해 저장 공간 활용도가 더 좋다.
💋 101차 B Tree로 알아보는 B Tree의 강력함!
✔️ 파라미터
- 최대 자녀 수 ⇒ 101개
- 최대 키 수 ⇒ 100개
- 최소 자녀 수 ⇒ 51개
- 최소 키 수 ⇒ 50개
✔️ best case
- 각 노드가 모두 최대 자녀 수와 최대 키 수를 가지는 경우
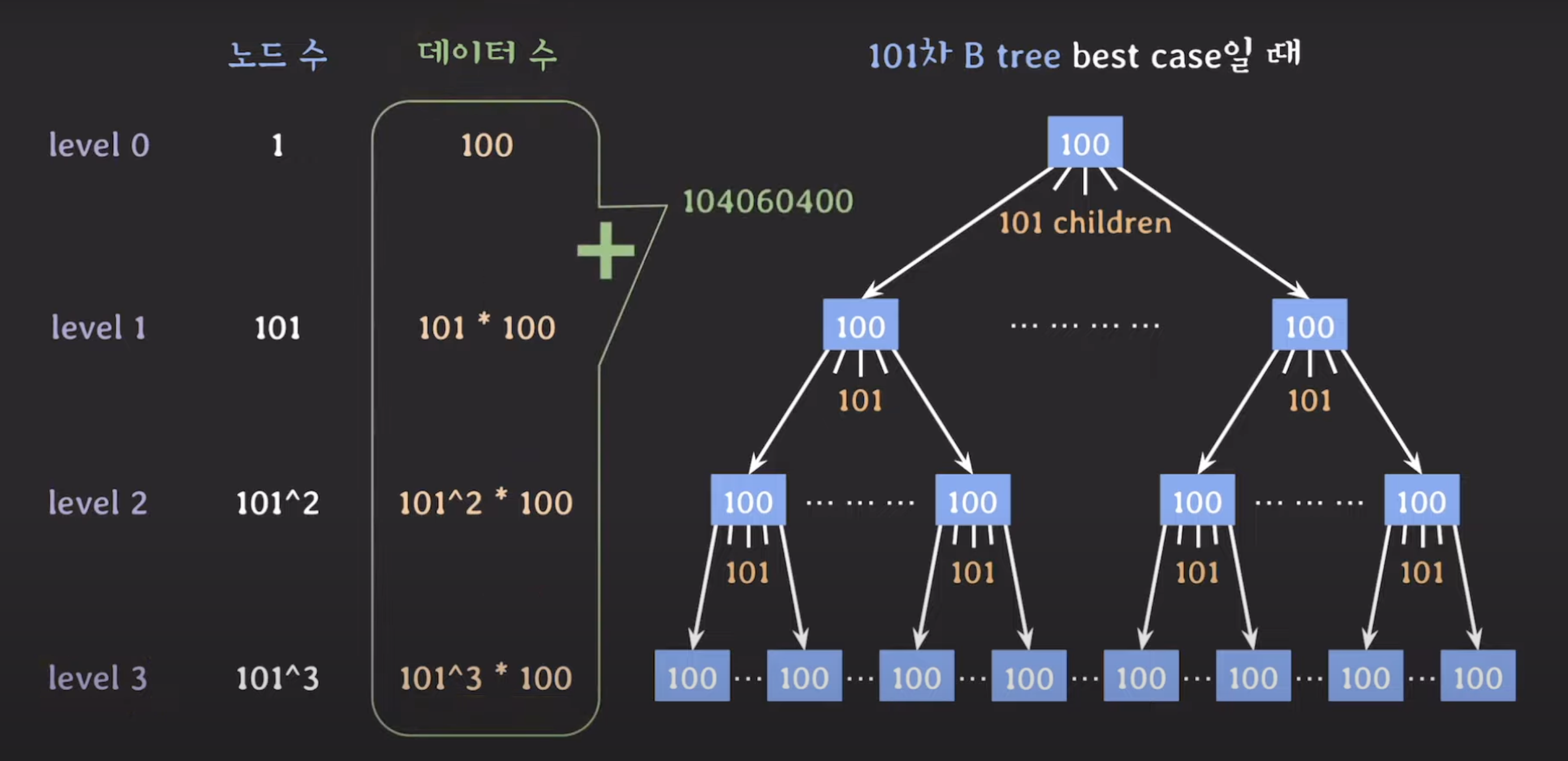
⇒ best case에서 약 1억 개의 데이터에 3번의 secondary storage 접근으로 모든 데이터를 탐색할 수 있다.
✔️ worst case
- 각 노드가 모두 최소 자녀 수와 최소 키 수를 가지는 경우
- root 노드는 제외되는 조건이므로, 루트 노드는 2개의 자녀와 1개의 키만 가져도 된다.
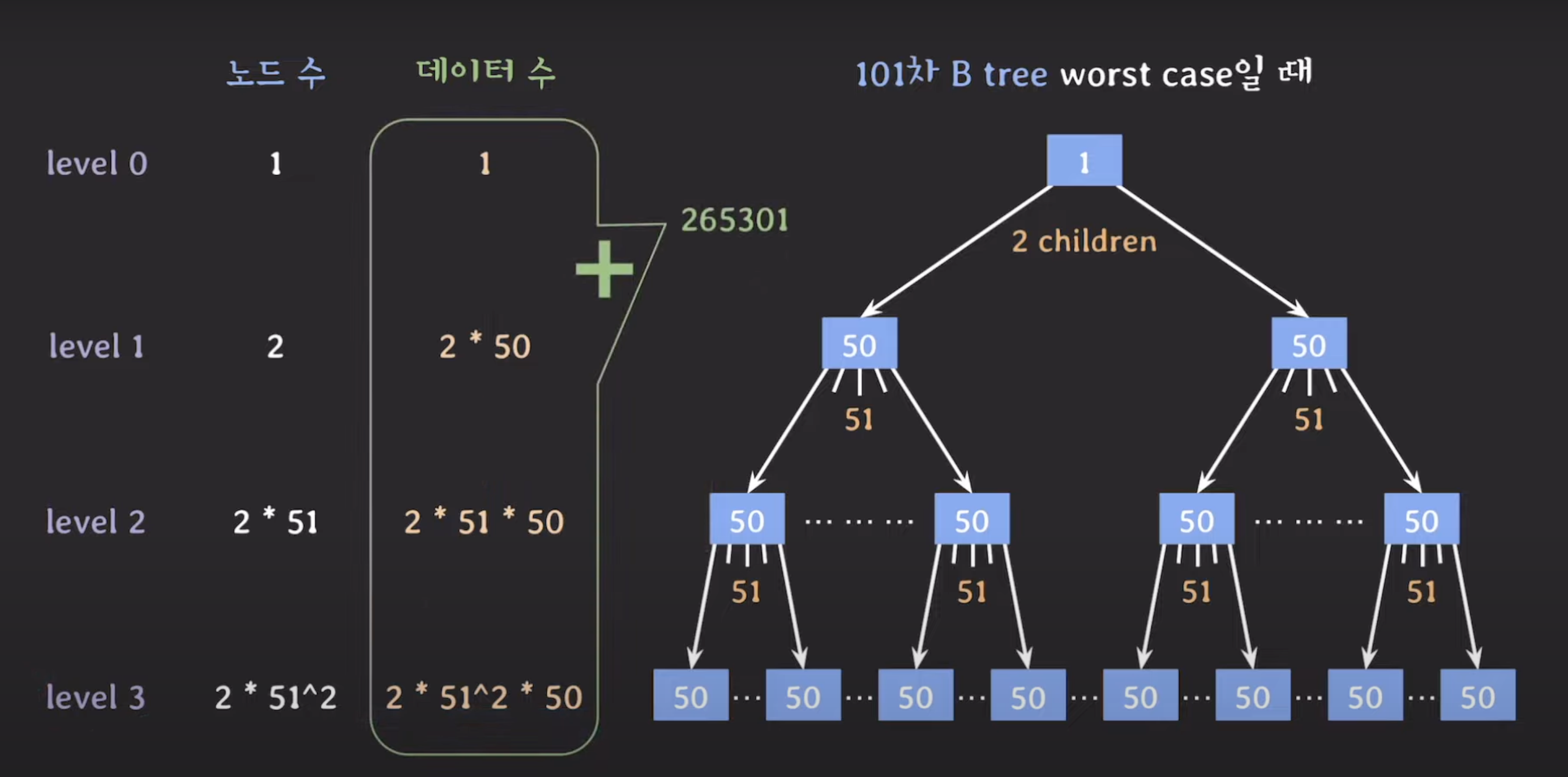
⇒ worst case에서도 약 26만 개의 데이터에 3번의 secondary storage 접근으로 모든 데이터를 탐색할 수 있다. (이정도면 우수함!)
✔️ average case

평균적인 경우에도 굉장히 큰 이점을 가진다!
💋 결론
- DB는 secondary storage에 저장된다.
- secondary storage는 데이터 처리 속도가 매우 느리기 때문에, 적게 접근할 수록 성능이 좋아진다.
- B Tree index는 self-balancing BST(AVL Tree, Red-Black Tree)에 비해서 secondary storage 접근을 적게 한다.
- B Tree index는 block 단위의 저장 공간을 더 알차게 사용할 수 있다.
💋 참고자료
- https://www.youtube.com/watch?v=liPSnc6Wzfk&list=PLcXyemr8ZeoR82N8uZuG9xVrFIfdnLd72&index=27
- https://www.youtube.com/watch?v=aZjYr87r1b8

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] Set과 HashSet: 개념, List vs Set (메모리와 iteration 속도 관점에서) (0) | 2023.12.20 |
|---|---|
| [자료구조] Map과 Hash Table: 해시 함수와 해시 충돌의 해결, 해시 테이블 리사이징 (3) | 2023.12.19 |
| [자료구조] B-Tree의 개념, 파라미터, 데이터 삽입, 삭제 과정을 알아보자! (2) | 2023.12.18 |
| [자료구조] AVL 트리의 개념, Balance Factor, 시간 복잡도와 한계에 대해 알아보자! (0) | 2023.12.17 |
| [자료구조] 이진 탐색 트리 (Binary Search Tree): 개념, 순회, 연산과 시간 복잡도 (2) | 2023.12.15 |
