Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS
GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip
주니어 개발자를 위한 전공 지식 모음.zip. Contribute to seoul-developer/CS development by creating an account on GitHub.
github.com
💋 이진 탐색 트리
✔️ 개념
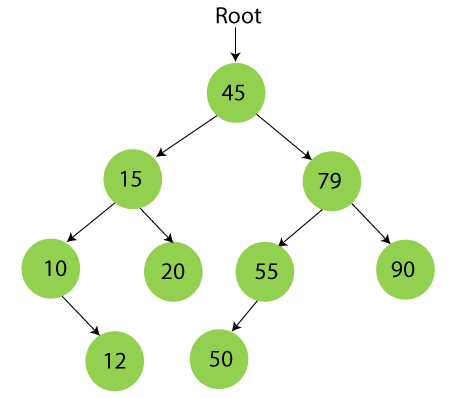
- 이진 트리 ⇒ 모든 노드가
최대 두 개의 자녀 노드를 가지는 트리 - 탐색 트리 ⇒ 모든 노드의 왼쪽 서브 트리는 노드의 값보다 작은 값만 가지고, 모든 노드의 오른쪽 서브 트리는 노드의 값보다 큰 값들만 가지는 트리
✔️ 특징
- 이진 탐색 트리의
최소값은 트리의 가장 왼쪽에 있다. - 이진 탐색 트리의
최대값은 트리의 가장 오른쪽에 있다.
💋 이진 탐색 트리의 순회 방법
이진 탐색 트리에서의 순회 방법은 다양하다.
(만약 왼쪽 자녀 노드를 L 현재 노드를 N 오른쪽 자녀 노드를 R 이라고 하면 총 6가지의 방문 순서가 있게된다. LNR LRN 등등…!)
그중 가장 자주 사용되는 3가지 대표적인 순회 방법에 대해 알아보자!
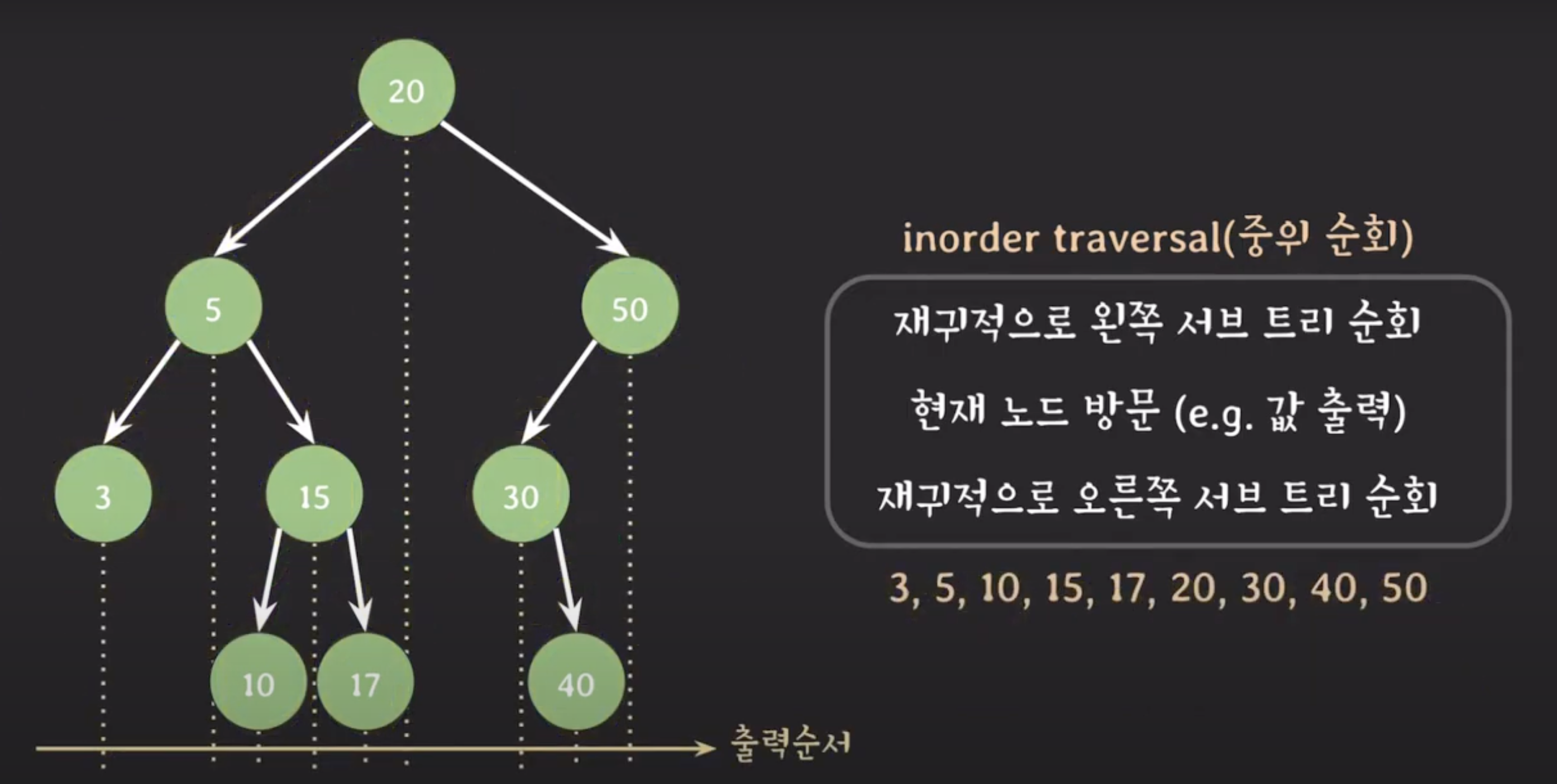
✔️ inorder traversal (중위 순회)
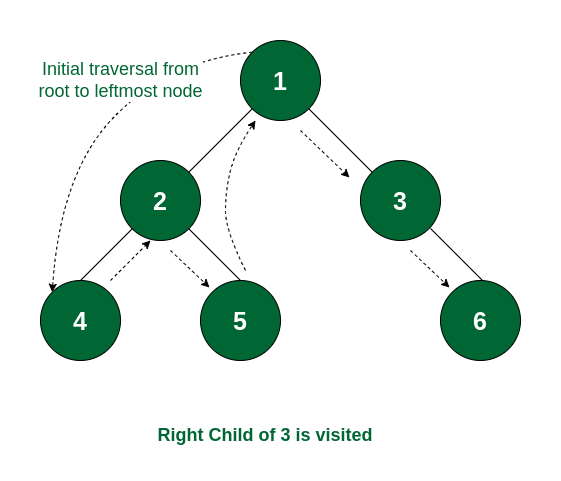

inorder traversal에서는 트리의 데이터를 왼쪽에서부터 순서대로 방문하게 된다.
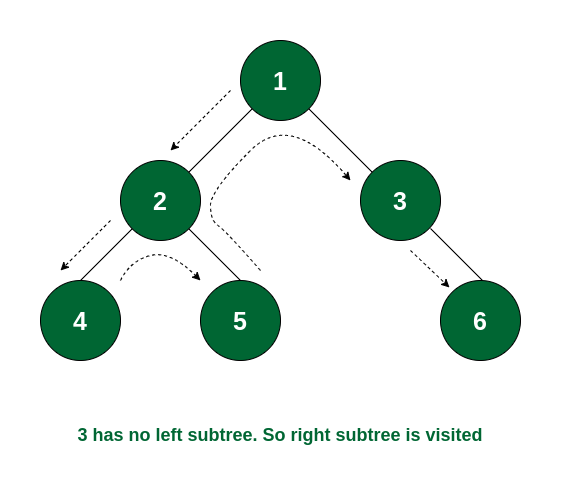
✔️ preorder traversal (전위 순회)

✔️ postorder traversal (후위 순회)
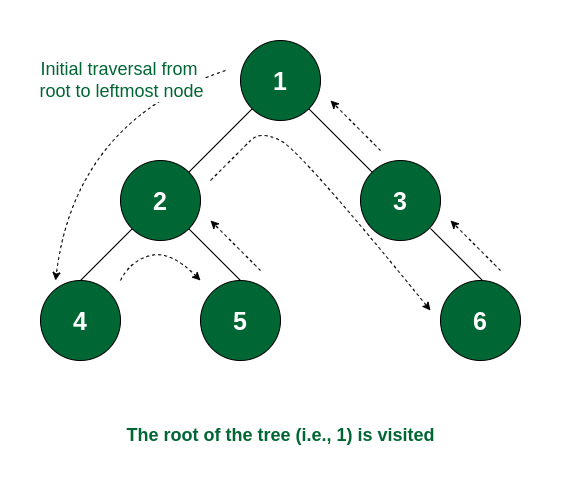

✔️ 비교

💋 노드의 successor (후임자)
- 현재 노드보다 값이 큰 노드 중에서 가장 값이 작은 노드
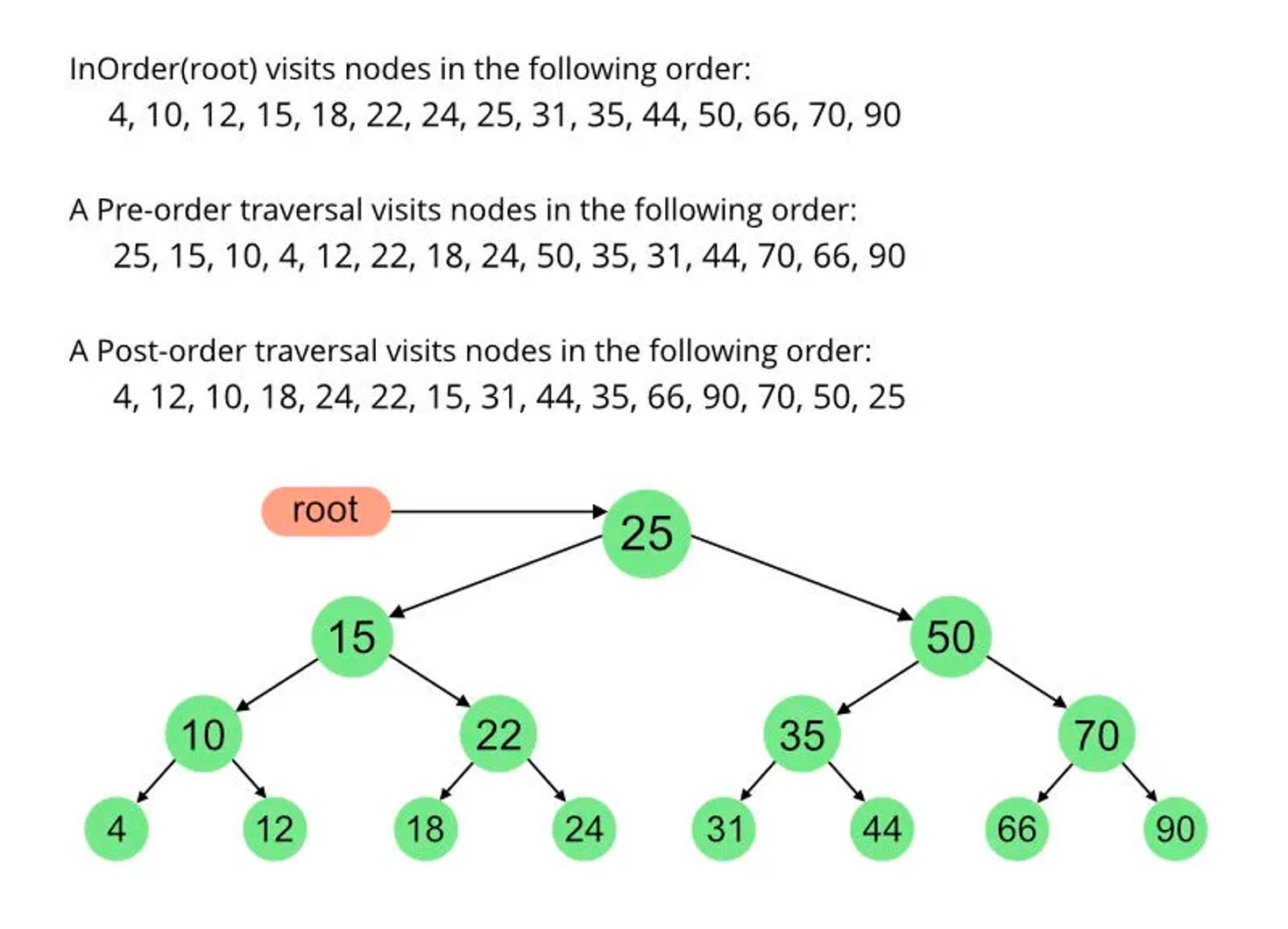
위 그림에서 4의 successor는 10이고, 10의 successor는 12, 12의 successor는 15, 15의 successor는 18이다.
이것은 inorder traversal에서 순회한 순서와 동일하다!!!
In Binary Tree, Inorder successor of a node is the next node in Inorder traversal of the Binary Tree. Inorder Successor is NULL for the last node in Inorder traversal. - geeksforgeeks
💋 이진 탐색 트리의 연산
✔️ 탐색
탐색은 아래의 과정에서 탐색에 성공할 때까지 계속해서 반복한다.
- 탐색하려는 값이 루트 노드의 키 값과 같으면 탐색에 성공한다.
- 탐색하려는 값이 루트 노드의 키 값보다 작으면 왼쪽 서브트리를 탐색한다.
- 탐색하려는 값이 루트 노드의 키 값보다 크면 오른쪽 서브트리를 탐색한다.
이 과정에서 데이터를 발견하지 못하면 탐색에 실패한다.
최악의 경우 시간 복잡도는 O(h) 인데, 여기서 h는 트리의 높이를 말한다. 여기서 최악의 경우는, 이진 탐색 트리가 변질 이진 트리에 가까운 모양을 한 경우이다.
트리의 모양이 균형 이진 트리 쪽에 가까울 수록 트리가 균형잡혔다고 하는데, 이 경우 h가 log(n) (n은 노드의 개수)에 가까워진다.
트리가 균형 잡힌 경우 ⇒ 탐색 시간 복잡도는 O(log n)
트리가 한쪽으로 치우쳐져 있을 경우 ⇒ 최악의 경우에 탐색 시간 복잡도는 O(n)
✔️ 삽입
먼저 삽입하려는 데이터를 탐색해야 한다. 데이터가 이미 존재한다면 삽입할 수 없기 때문에, 탐색을 하다가 실패해 NULL을 반환받은 그 위치에 데이터를 삽입한다.
오래 걸리는 작업은 데이터를 탐색이기 하기 때문에, 탐색과 동일한 시간 복잡도를 가진다.
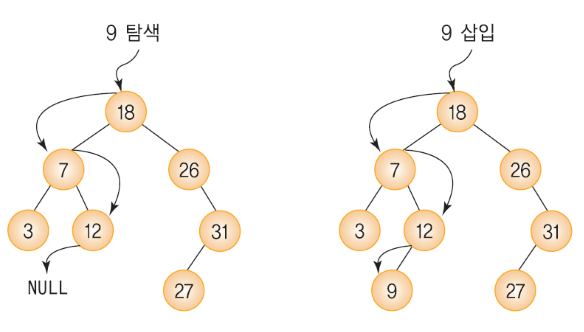
[개인적 궁금증] 이진 탐색 트리에 중복값을 저장하면 어떻게 될까?
오른쪽 서브트리(또는 왼쪽서브트리)에 중복 키를 허용하는 방식으로 해결할 수 있다.
트리 규칙을 left sub-tree <= node < right sub-tree와 같이 수정하면 간단히 구현할 수 있게 되지만, 효율적인 탐색이 어렵게 될 수 있다.
다른 방법으로는 노드에 해당 키의 개수를 의미하는 count도 함께 저장하는 방법을 생각해볼 수도 있다.
참고로, 일반적으로 많은 알고리즘은 중복이 제외된다고 명시한다. 중복 가능을 구현하는 것은 간단한 작업이며, 학습 과정에서 중복 노드가 허용되는 경우 불필요한 계산 단계가 추가로 필요하기 때문에 그냥 '중복은 허용되지 않는다'고 생각하고 학습해도 충분할 것 같다.
✔️ 삭제
삭제 연산은 조금 복잡하다.
- 삭제할 노드가 리프 노드인 경우
- 삭제할 노드가 1개의 자녀 노드만 가지고 있는 경우
- 삭제할 노드가 2개 이상의 자녀 노드를 가지고 있는 경우
삭제할 노드가 리프 노드인 경우 ⇒ 삭제될 노드를 가리키던 레퍼런스를 가리키는 것이 없도록(NULL) 처리
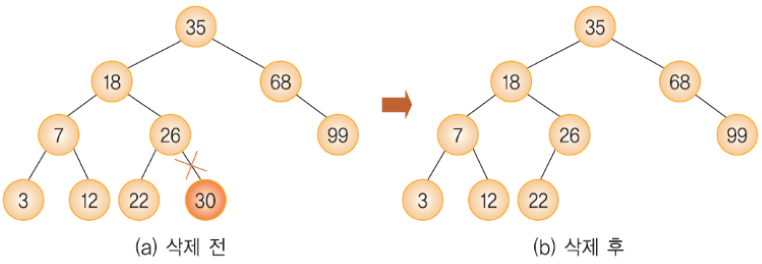
삭제할 노드가 1개의 자녀 노드만 가지고 있는 경우 ⇒ 삭제될 노드를 가리키던 레퍼런스를 삭제될 노드의 자녀 노드를 가리키도록 변경

삭제할 노드가 2개 이상의 자녀 노드를 가지고 있는 경우 ⇒ 삭제될 노드의 오른쪽 서브 트리에서 제일 값이 작은 노드가 삭제될 노드를 대체한다. (왼쪽 서브트리에서 제일 값이 큰 값도 괜찮음)
삭제를 하고 나서도, 여전히 이진 탐색 트리의 특징이 유지될 수 있도록 레퍼런스를 조정하는 과정이 필요하다.
삭제 작업 역시 데이터 탐색을 동반하기 때문에 탐색과 동일한 시간 복잡도를 가진다.
💋 이진 탐색 트리의 시간 복잡도
✔️ Best Case
삽입/삭제/탐색할 데이터가 루트 노드에 위치한 경우에는 곧바로 처리할 수 있어서, Θ(1)의 시간 복잡도를 가진다.
관련해서는, 아래 댓글을 참고하면 자세히 설명이 되어 있다!
✔️ Average Case

이진 트리가 어느 정도 균형이 잡혀 있는 경우에는, 한 번의 탐색에서 트리의 절반씩을 줄여 나갈 수 있어서, O(logN)의 시간 복잡도를 가진다.
✔️ Worst Case
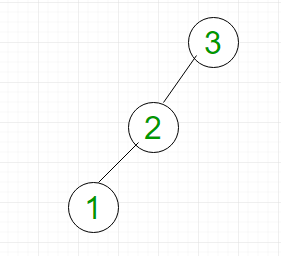
이진 트리가 완전히 한쪽으로 치우쳐 있는 변질 이진 트리와 유사한 형태인 경우에는 루트 노드에서 출발해 트리의 모든 노드를 확인해야 하기 때문에 O(n)의 시간 복잡도를 가진다.
💋 이진 탐색 트리의 장점/단점
✔️ 장점
- 삽입/삭제가 유연하다. ⇒ 레퍼런스만 재조정하면 된다.
- 값의 크기에 따라서 좌우로 서브트리가 나눠지기 때문에 삽입/삭제/검색이 (일반적으로) 빠르다.
- 일반적으로 = 변질 이진 트리처럼 너무 치우치지 않는 경우
- 값을 순서대로 순회할 수 있다.
✔️ 단점
- 트리가 구조적으로 한쪽으로
편향되면 모든 동작의 수행 시간이 악화된다. - 이진 탐색 트리가 변질 이진 트리에 가까운 모양으로 (한쪽으로 치우쳐) 생긴 경우에, 삽입/삭제/탐색에
O(n)의 시간 복잡도를 가진다. ⇒ 오래 걸린다.
⇒ 트리가 편향된 경우에 발생하는 문제를 해결하기 위해서, 스스로 균형을 잡는 이진 탐색 트리가 사용된다.
⇒ AVL 트리, Red-Black 트리 (worst case에도 삽입/삭제/탐색의 시간복잡도가 O(logN)다.)
💋 참고자료
- https://www.geeksforgeeks.org/binary-search-tree-data-structure/
- https://praharshbhatt.medium.com/everything-about-tree-traversal-inorder-preorder-postorder-time-complexity-with-code-2f4de533277f
- https://www.geeksforgeeks.org/inorder-traversal-of-binary-tree/
- https://www.geeksforgeeks.org/preorder-traversal-of-binary-tree/
- https://www.geeksforgeeks.org/postorder-traversal-of-binary-tree/
- https://stackoverflow.com/questions/300935/are-duplicate-keys-allowed-in-the-definition-of-binary-search-trees
- https://github.com/hectick/CS/blob/irene/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0/Binary%20Search%20Tree.md#%EC%9D%B4%EB%AF%B8-%EC%A1%B4%EC%9E%AC%ED%95%98%EB%8A%94-%ED%82%A4%EC%99%80-%EC%A4%91%EB%B3%B5%EB%90%9C-%ED%82%A4%EB%A5%BC-%EC%82%BD%EC%9E%85%ED%95%B4%EC%95%BC-%ED%95%A0-%EA%B2%BD%EC%9A%B0

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] B-Tree의 개념, 파라미터, 데이터 삽입, 삭제 과정을 알아보자! (2) | 2023.12.18 |
|---|---|
| [자료구조] AVL 트리의 개념, Balance Factor, 시간 복잡도와 한계에 대해 알아보자! (0) | 2023.12.17 |
| [자료구조] Priority Queue(우선순위 큐)와 Heap(힙) (2) | 2023.12.15 |
| [자료구조] 이진 트리(Binary Tree): 트리의 분류와 이진 트리의 종류(Full, Complete, Perfect, Balanced, Degenarate Binary Tree) (0) | 2023.12.14 |
| [자료구조] 트리(Tree) 구조의 개념, 용어, 특징에 대해 알아보자! (5) | 2023.12.14 |
