Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS
GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip
주니어 개발자를 위한 전공 지식 모음.zip. Contribute to seoul-developer/CS development by creating an account on GitHub.
github.com
💋 인트로
앞선 이진 탐색 트리에 관한 포스팅에서 마지막에 소개한 단점에 대한 부분에 주목해보자.
- 이진 탐색 트리는 트리가 구조적으로 한쪽으로
편향되면 모든 동작의 수행 시간이 악화된다. - 이진 탐색 트리가 변질 이진 트리에 가까운 모양으로 (한쪽으로 치우쳐) 생긴 경우에, 삽입/삭제/탐색에
O(n)의 시간 복잡도를 가진다. ⇒ 오래 걸린다.
⇒ 트리가 편향된 경우에 발생하는 문제를 해결하기 위해서, 스스로 균형을 잡는 이진 탐색 트리가 사용된다.
⇒ AVL 트리, Red-Black 트리 (worst case에도 삽입/삭제/탐색의 시간복잡도가 O(logN)다.)
이렇게 트리가 한쪽으로 편향되는 경우 생기는 성능의 문제를 개선하기 위해 등장한 개념인 AVL 트리와 Red-Black 트리 중에서 오늘 포스팅에서는 AVL 트리에 대해 알아보자!
💋 AVL 트리
✔️ 개념
- 이진 탐색 트리(BST)의 한 종류
- 스스로 균형을 잡는 트리
- balance factor를 통해서 균형을 유지한다.
이름이 왜 AVL인지 궁금한데, Adelson-Velsky and Landis 이 세 사람이 발명해서 각자 하나씩 붙였다고 한다. 아 내가 발명해서 깃짱트리라고 했어야 하는데
An AVL tree defined as a self-balancingBinary Search Tree(BST) where the difference between heights of left and right subtrees for any node cannot be more than one. - geeksforgeeks

✔️ balance factor
임의의 노드에 대해서, 노드의 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차를 Balance Factor라고 한다.
In a binary tree the balance factor of a node X is defined to be the height difference - wikipedia
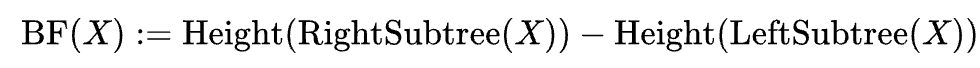
AVL 트리에서는 모든 노드에 대해서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차가 0 또는 1만 허용하기 때문에, Balance Factor는 -1, 0, 1 셋 중 하나가 된다고 볼 수 있다.
아래 식은 AVL 트리 내 모든 노드 x에 대해서 성립한다.

BF(X)가 0보다 작을 때 노드 X를 "left-heavy"라고 하며, BF(X)가 0보다 클 때는 "right-heavy"라고 한다. BF(X)가 0일 때는 종종 "balanced"라고 간단히 말한다.
💋 AVL 트리의 연산
트리에 삽입/삭제 작업이 일어나는 경우에, 루트 노드에서 적절한 위치까지 찾아가 처리를 하고, 삽입/삭제가 발생한 위치에서 루트 노드로 거꾸로 올라오면서 balance factor가 -1, 0, 1을 벗어나는 노드가 생기면 균형을 맞추는 재조정 작업을 수행한다.
✔️ Left Rotation
node C를 삽입한 후에 node A의 입장에서 BF를 계산해보면 BF(A) = -1 -1 = -2로 균형이 깨졌다!
B를 가운데 놓으면서 A를 왼쪽 서브트리로 보내면 이진 탐색 트리의 구조를 만족하면서도, 균형을 맞출 수 있게 된다.
왼쪽으로 회전시킨다는 의미에서 Left Rotation이라고도 한다.

✔️ Right Rotation
아래 상황을 생각해보자.
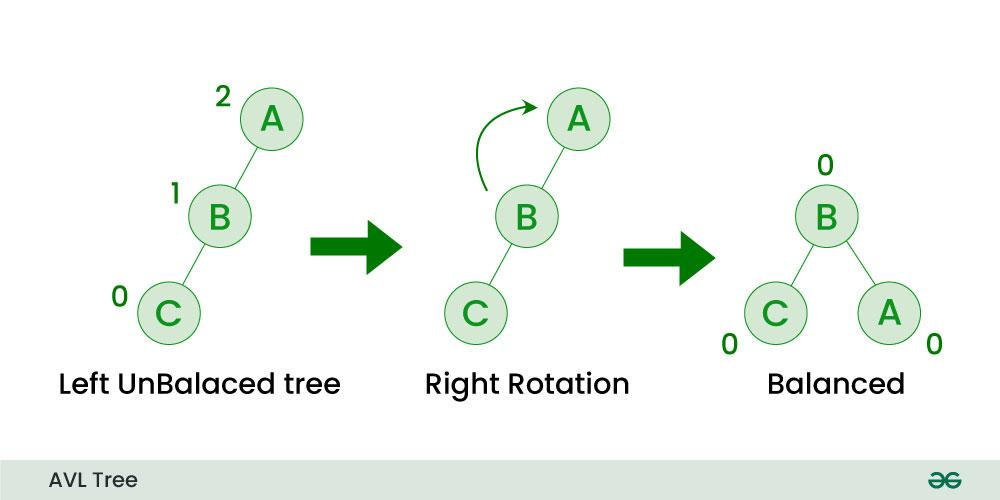
node 30을 넣었더니, BF(70) = 2 - 0 = 2로 균형이 깨져버렸다. ⇒ Left Unbalanced Tree

아까와 같이 50을 70 위로 올려주면 된다.

아래 그림과 같이 Right Rotation을 통해서 균형을 맞추었다고 볼 수 있다.
💋 AVL 트리의 시간 복잡도

이진 탐색 트리와 비교했을 때, best case와 average case는 동일하지만, worst 케이스의 경우에도 O(n)이 아니라 O(logN)으로 개선되었다.
⇒ 최악의 경우에도 삽입/삭제/검색의 시간 복잡도는 O(logN)이다.
💋 AVL 트리의 한계
엄격하게 균형을 유지하기 때문에, 삽입/삭제 시 트리 균형을 확인하고 균형이 깨졌다면 트리 구조를 재조정하기 때문에 시간이 꽤나 소요된다는 한계가 있다.
⇒ 이 문제는 Red-Black 트리가 해결했다.
💋 참고자료
- https://www.geeksforgeeks.org/introduction-to-avl-tree/
- https://en.wikipedia.org/wiki/AVL_tree
- https://www.youtube.com/watch?v=syGPNOhsnI4&list=PLcXyemr8ZeoR82N8uZuG9xVrFIfdnLd72&index=10

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!
