[자료구조] Priority Queue(우선순위 큐)와 Heap(힙)

반응형

 

 

Computer Science 모아보기 👉🏻 https://github.com/seoul-developer/CS

GitHub - seoul-developer/CS: 주니어 개발자를 위한 전공 지식 모음.zip

 

💋 Priority Queue vs Heap

두 가지를 VS로 놓긴 했지만, 실은 우선순위 큐는 추상이고, 힙은 구현이다.

우선순위 큐 ADT는 자료구조의 개념과 주요기능만을 정의하고, 구체적인 구현은 힙으로 나타난다.

 

💋 Priority Queue(우선순위 큐) ADT

✔️ 개념

• 우선순위가 높은 데이터가 먼저 처리되는 큐
• 각 데이터에 우선순위를 할당하고 그 우선순위에 따라 데이터에 접근할 수 있는 자료구조
• 큐(Queue)와 비슷하지만, 큐는 선입선출(FIFO, First-In-First-Out)의 원칙에 따라 데이터를 처리하는 반면, 우선순위 큐는 데이터의 우선순위에 따라 데이터를 처리한다.
• 주로 최소값 또는 최대값을 빠르게 찾아야 하는 상황에서 활용된다.
• 프로세스 스케줄링, 그래프 알고리즘, 네트워크 라우팅 등

 

✔️ 주요 동작

• insert
• 새로운 데이터를 우선순위 큐에 추가합니다.
• 이때 데이터는 해당 우선순위에 따라 정렬됩니다.
• delete
• 가장 높은 우선순위를 가진 데이터를 큐에서 제거합니다.
• 최소값 우선순위 큐의 경우에는 최소값이, 최대값 우선순위 큐의 경우에는 최대값이 삭제됩니다.
• peek
• 현재 큐에서 가장 높은 우선순위 또는 가장 낮은 우선순위를 가진 데이터를 조회합니다.

 

✔️ 구현체

우선순위 큐는 배열, LinkedList, Heap 자료구조, Binary Search Tree 등등 다양한 방법으로 구현할 수 있다.

 

 

무튼 결과적으로 위에서 볼 수 있듯 이중에서 Heap으로 구현하는게 효율적이다.

 

💋 Heap(힙)

✔️ 개념

• 우선순위 큐를 구현하는 하나의 방법이다.
• 부모 노드의 우선순위가 자식 노드의 우선순위보다 항상 높은 완전 이진 트리 로 구현된 우선순위 큐

A Heap is a special Tree-based Data Structure in which the tree is a complete binary tree.

 

출처: 이리내

• Parent-Child Relationship
• 완전 이진 트리이기 때문에 (마지막 레벨을 제외하고는 빈틈이 없이 노드가 다 채워져 있음) 부모 노드의 인덱스를 i라고 했을 때, 자녀 노드의 인덱스를 알 수 있습니다. (노드 번호는 1부터 시작하는 인덱스 기준)
• 왼쪽 자식은 인덱스 2i
• 오른쪽 자식은 인덱스 2i + 1

 

 

✔️ 종류

 

위에서는 부모 노드의 우선순위가 자식 노드의 우선순위보다 항상 높다고 했지만, 힙의 종류에 따라서 그 반대가 될 수도 있다.

 

• Max Heap
• 부모 노드의 키(key)가 자식 노드의 키(key)보다 항상 크거나 같은 트리
• 부모 노드의 우선순위가 항상 자식 노드의 우선순위보다 크거나 같다.

 

• Min Heap
• 부모 노드의 키(key)가 자식 노드의 키(key)보다 항상 작거나 같은 트리
• 부모 노드의 우선순위가 항상 자식 노드의 우선순위보다 작거나 같다.

 

✔️ 특징

• 완전 이진 트리(Complete Binary Tree)
• 힙 트리는 마지막 레벨을 제외하고는, 모든 레벨이 가득 차 있는 완전 이진 트리입니다. (마지막 레벨은 가능한 한 왼쪽부터 차있을 수 있음)
• 중간이 비어있지 않음 ⇒ 배열을 사용하여 효율적으로 구현
• Heap Property
• 트리의 루트는 항상 최소값 또는 최대값

 

💋 Heap의 연산

연산은 모두 Max Heap 기준으로 설명하겠습니다. Min Heap은 그냥 반대로 생각하면 됩니다.

 

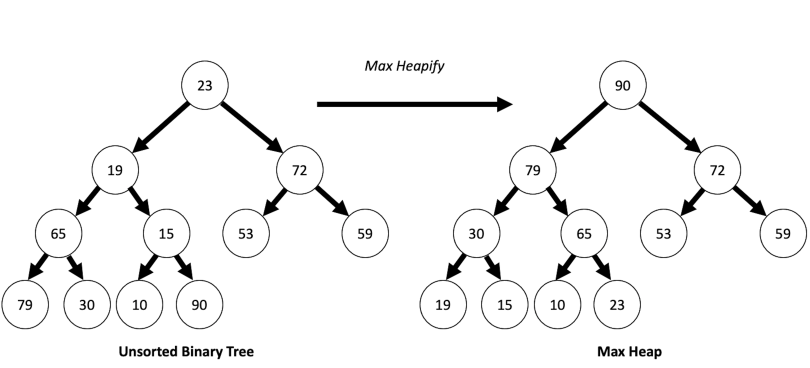
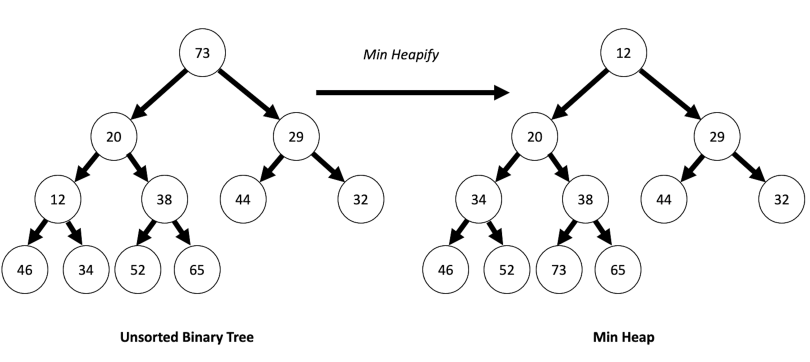
✔️ Heapify

• 힙 자료 구조의 속성을 유지하도록 요소를 재배치하는 과정
• 여기서 말하는 속성은 완전 이진 트리이면서, 부모 노드의 키가 자식 노드의 키보다 항상 크거나 같은 것을 말한다.
• 일부 작업(데이터 추가, 삭제)으로 인해 힙에서 완전 이진트리가 깨지거나, 부모 노드의 키가 자식 노드의 키보다 작아지는 불균형이 생기는 경우에 바로잡기 위한 작업이다.
• O(log N)의 시간이 소요된다.

 

 

✔️ Insertion

1. 힙의 크기를 1만큼 증가시킨다.
2. 리프 레벨의 맨 마지막 노드에 새로운 데이터를 저장한다.
3. Heapify 작업을 수행한다. ⇒ upheap 반복

 

• upheap: 부모 노드와 비교해, 부모 노드가 우선순위가 더 낮으면 부모 노드와 키를 교환하는 작업
• 트리의 균형이 맞을 때까지 다시 Heapify 과정을 반복해야 하므로, 결과적으로 O(log N)의 시간이 소요된다.

 

 

✔️ Deletion

• 이진 힙에서의 삭제는 우선순위가 가장 높은 루트가 삭제되는 것이다.

 

1. 루트가 삭제된다.
2. 루트의 데이터를 대체하기 위해 가장 마지막 노드를 루트에 옮긴다.
3. 힙 크기를 1만큼 줄인다.
4. Heapify 작업을 수행한다. ⇒ downheap 반복

 

• downheap: 자식 노드 중 우선순위가 높은 노드와 비교해, 자식 노드가 우선순위가 더 높다면 자식 노드와 키를 교환하는 작업

 

• 트리의 균형이 맞을 때까지 다시 Heapify 과정을 반복해야 하므로, 결과적으로 O(log N)의 시간이 소요된다.

 

 

✔️ getMax

(min heap의 경우 getMin)

 

• 최대값은 항상 루트 노드에 있으므로, 루트 노드의 값을 가져오면 된다. ⇒ O(1)

 

 

 

💋 참고자료

• https://www.geeksforgeeks.org/introduction-to-heap-data-structure-and-algorithm-tutorials/?ref=ghm
• https://www.youtube.com/watch?v=P-FTb1faxlo&list=PLcXyemr8ZeoR82N8uZuG9xVrFIfdnLd72&index=2
• https://www.geeksforgeeks.org/priority-queue-set-1-introduction/
• https://www.programiz.com/dsa/priority-queue
• https://chanhuiseok.github.io/posts/ds-4/
• https://www.youtube.com/watch?time_continue=599&v=cuL8gXCSA58&embeds_referring_euri=https%3A%2F%2Fbuiltin.com%2F&source_ve_path=MTM5MTE3LDI4NjYzLDI4NjYzLDI4NjYzLDIzODUx&feature=emb_title

 

도움이 되었다면, 공감/댓글을 달아주면 깃짱에게 큰 힘이 됩니다!🌟
비밀댓글과 메일을 통해 오는 개인적인 질문은 받지 않고 있습니다. 꼭 공개댓글로 남겨주세요!